The orbital speed of a satellite revolving around a planet in a circular orbit is v0 . If its speed is increased by 10 % ,then
It will escape from its orbit
It will start rotating in an elliptical
It will continue to move in the same orbit
It will move in a circular orbit of radius 20 % more than radius of intial orbit
The correct Answer is:B
To solve the problem, we need to analyze the effect of increasing the orbital speed of a satellite by 10%. Let's break it down step by step.
Step 1: Understand the initial conditions
The initial orbital speed of the satellite is given as v0. The orbital speed for a satellite in a circular orbit around a planet is determined by the formula:
v0=√GMR
where G is the gravitational constant, M is the mass of the planet, and R is the radius of the orbit.
Step 2: Calculate the new speed
If the speed is increased by 10%, the new speed v can be calculated as:
v=v0+0.1v0=1.1v0
Step 3: Determine the relationship between the new speed and escape velocity
The escape velocity ve from the planet is given by:
ve=√2v0
To find out if the new speed v is less than, equal to, or greater than the escape velocity, we need to compare 1.1v0 with ve:
ve=√2v0≈1.414v0
Since 1.1v0<1.414v0, we conclude that:
v<ve
Step 4: Determine the type of orbit
Since the new speed v is greater than the original orbital speed v0 but less than the escape velocity ve, the satellite will no longer be in a circular orbit. Instead, it will enter an elliptical orbit.
Conclusion
Thus, the satellite will start rotating in an elliptical orbit.
Final Answer
The correct conclusion is: It will start rotating in an elliptical orbit.
---
The initial orbital speed of the satellite is given as v0. The orbital speed for a satellite in a circular orbit around a planet is determined by the formula:
v0=√GMR
where G is the gravitational constant, M is the mass of the planet, and R is the radius of the orbit.
If the speed is increased by 10%, the new speed v can be calculated as:
v=v0+0.1v0=1.1v0
The escape velocity ve from the planet is given by:
ve=√2v0
To find out if the new speed v is less than, equal to, or greater than the escape velocity, we need to compare 1.1v0 with ve:
ve=√2v0≈1.414v0
Since 1.1v0<1.414v0, we conclude that:
v<ve
Since the new speed v is greater than the original orbital speed v0 but less than the escape velocity ve, the satellite will no longer be in a circular orbit. Instead, it will enter an elliptical orbit.
Thus, the satellite will start rotating in an elliptical orbit.
The correct conclusion is: It will start rotating in an elliptical orbit.
Topper's Solved these Questions
- GRAVITATION BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - C (PREVIOUS YEARS QUESTIONS)
52 Videos
- GRAVITATION BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
16 Videos
- GRAVITATION BOOK - AAKASH INSTITUTECHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - A (OBJECTIVE TYPE QUESTIONS)
49 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTECHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
13 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTECHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
Similar Questions
Knowledge Check
A satellite is revolving round the earth in circular orbit
Aif mass of earth is made four times, keeping other factors constant, orbital speed of satellite will become two timesBcorresponding to change in part(a), times period of satellite will become halfCwhen value of G is made two times orbital speed increases and time period decreasesDG has no effect on orbital speed and time periodThe orbital speed of geostationary satellite is around
A3.07 km/sB7.95 km/sC11.2 km/sD15.8 km/sIf L is the angular momentum of a satellite revolving around earth is a circular orbit of radius r with speed v , then
AL∝vBL∝rCL∝√rDL∝√v
Consider a hypothetical planet which is very long and cylinderical. The density of the planet is ρ, its radius is R.

What is the possible orbital speed of the satellite in moving around the planet in circular orbit in a plane which is perpendicular to the axis of planet?
View SolutionA satellite revolves around the earth in an elliptical orbit. Its speed is
View SolutionA satellite revolves around the earth in elliptic orbit ,its speed is :
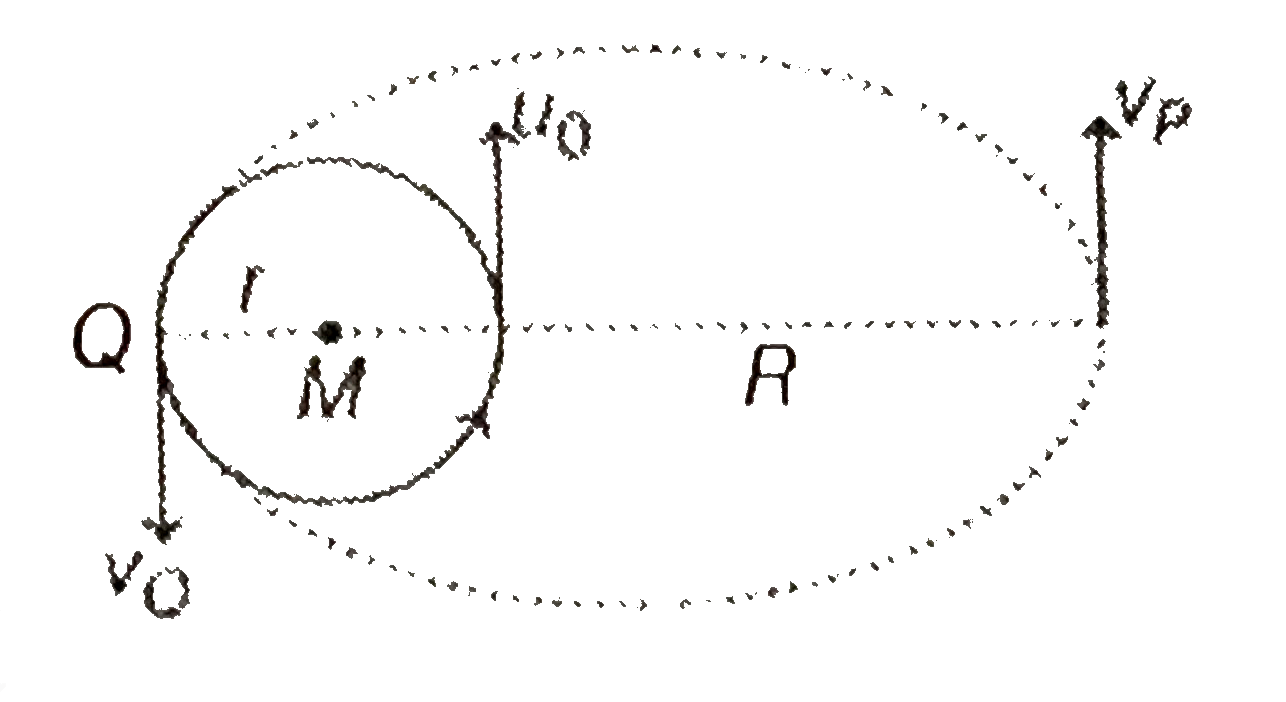
View SolutionA light satellite is initially rotating around a planet in a circular orbit of radius r. Its speed in this circular orbit was u0. It is put in an elliptical orbit by increasing its speed form u0 to vQ ( instantaneously). In the elliptical orbit, the satellite reaches the farthest point P, which is at a distance R from the planet. Satellite's speed at farthest point is vP. At point Q, the speed required by satellite to escape the planet's gravitational pull is vesc
View SolutionA satellite is revolving round the earth in an elliptical orbit. Its speed will be
View Solution
