A square card of side length 1 mm is being seen through a magnifying lens of focal length 10 cm. The card is placed at a distance of 9 cm from the lens. The appaent area of the card thorugh the lens is
1cm2
0.81cm2
0.27cm2
0.60cm2
The correct Answer is:A
To solve the problem, we will follow these steps:
Step 1: Calculate the area of the square card.
The area A of a square is given by the formula:
A=side×side
Given that the side length of the card is 1 mm, we can calculate the area:
A=1mm×1mm=1mm2
Step 2: Identify the given values.
- Focal length of the lens f=10cm
- Object distance u=−9cm (the negative sign indicates that the object is on the same side as the incoming light)
Step 3: Use the lens formula to find the image distance v.
The lens formula is:
1v=1f+1u
Substituting the known values:
1v=110+1−9
Calculating the right side:
1v=110−19
Finding a common denominator (which is 90):
1v=990−1090=−190
Thus,
v=−90cm
Step 4: Calculate the magnification m.
Magnification is given by the formula:
m=−vu
Substituting the values we found:
m=−−90−9=10
Step 5: Calculate the apparent area of the card through the lens.
The apparent area A′ through the lens can be calculated using the magnification:
A′=m2×A
Substituting the magnification and the area of the card:
A′=102×1mm2=100mm2
Step 6: Convert the area to cm².
Since 1cm2=100mm2:
A′=1cm2
Thus, the apparent area of the card through the lens is 1cm2.
---
The area A of a square is given by the formula:
A=side×side
Given that the side length of the card is 1 mm, we can calculate the area:
A=1mm×1mm=1mm2
- Focal length of the lens f=10cm
- Object distance u=−9cm (the negative sign indicates that the object is on the same side as the incoming light)
The lens formula is:
1v=1f+1u
Substituting the known values:
1v=110+1−9
Calculating the right side:
1v=110−19
Finding a common denominator (which is 90):
1v=990−1090=−190
Thus,
v=−90cm
Magnification is given by the formula:
m=−vu
Substituting the values we found:
m=−−90−9=10
The apparent area A′ through the lens can be calculated using the magnification:
A′=m2×A
Substituting the magnification and the area of the card:
A′=102×1mm2=100mm2
Since 1cm2=100mm2:
A′=1cm2
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:NCERT FINGERTIPSChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:Refraction Through A Prism
Explore 9 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:NCERT FINGERTIPSChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:Some Natural Phenomena Due To Sunlight
Explore 2 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:NCERT FINGERTIPSChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:Total Internal Reflection
Explore 7 Videos
- PRACTICE PAPPERBook:NCERT FINGERTIPSChapter:PRACTICE PAPPERExercise:Practice Paper 3
Explore 50 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS Book:NCERT FINGERTIPSChapter:SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS Exercise:Assertion And Reason
Explore 15 Videos
Similar Questions
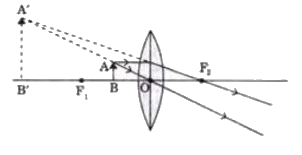
The above lens has a focal length of 10 cm. The object of height 2 mm is placed at a distance of 5 cm from the pole. Find the height of the image.
View SolutionA convex lens has a focal length of 10 cm. The object of height 2 mm is placed at a distance of 5 cm from the pole. Find the height of the image.
View Solution
Knowledge Check
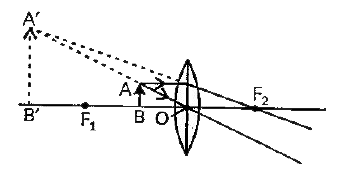
The above lens has a focal length of 10 cm. The object of height 2 mm is placed at a distance of 5 cm from the pole. Find the height of the image.A4 cmB6.67 mmC4 mmD3.33 mmA convex lens of focal length 15 cm is placed on a plane mirror. An object is placed at 30 cm from the lens. The image is
Areal, at 30 cm in front of the mirrorBreal, at 30 cm behind the mirrorCreal, at 10 cm in front of the mirrorDvirtual, at 10 cm behind the mirrorAn object is kept at a distance of 15 cm from a convex lens of focal length 10 cm. Calculate the image distance and state the characteristics of the image formed.
Aupright and magnifiedBinverted and magnifiedCinverted and diminishedDupright and diminished
The focal length of convex lens is 20 cm. If an object of height 4 cm is placed at a distance of 30 cm from the lens, find:
The height of the image
View SolutionA needle 10 cm long is placed along the axis of a convex lens of focal length 10 cm such that the middle point of the neddle is at a distance of 10 cm from the lens. Find the length of the image of the neddle.
View SolutionThe focal length of convex lens is 20 cm. If an object of height 4 cm is placed at a distance of 30 cm from the lens, find:
The position of the image
View SolutionThe focal length of convex lens is 20 cm. If an object of height 4 cm is placed at a distance of 30 cm from the lens, find:
The magnification produced by the lens.
View SolutionA convex lens of focal length 10 cm is placed in contact with a concave lens of focal length 20 cm. The focal length of this combination of lenses will be:
View Solution