Question

Obtain an expression for the electric field intenstiy at a point on the equatorial line of an electric dipole.

Explanation

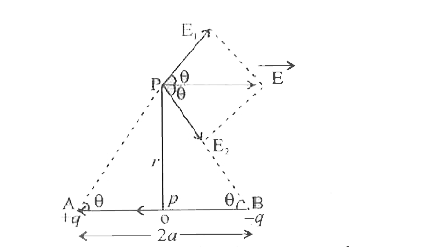
Consider an electric dipole consisting of two point charges +q and -q , separated by a small distance 2a.
To find the electric field intensity at P on the equatorial line of the dipole . When OP=r, `E_l` the electric field intensity at P due to charge +q is
`(E_1)=1/(4piepsilon_0)q/(AP^2) " " because AP^2 = a^2 + r^2`
`(E_1)=1/(4piepsilon_0) q/(a^2+r^2)`
The magnetic of the electric field intensity `E_2` at P due to charge -q is
`(E_2)=1/(4piepsilon_0) q/(a^2+r^2)`
The direction of `vecE_1` is away from the charge +q and the direction of `vecE_2` is towards the charge -q as shown .
`vecE_1` and `vecE_2` can be resolved into two components . The components normal to the dipole axis cancel away each other each being equal and opposite . The components along the dipole axis add up.
`therefore vecE_1=(E_1 cos theta + E_2 cos theta) - hatP`
Here the direction of `vecE` is opposite to dipole moment P. `therefore -hatP` is unit vector.
`vecE=(E_1+E_2)cos theta -hatP`
From the figure , `cos theta = a/((r^2+a^2)^(1//2))`
`vecE=[1/(4piepsilon_0)q/((a^2+r^2))+1/(4piepsilon_0) q/((a^2+r^2))]a/((a^2+r^2)^(1//2))-hatP`
`vecE=1/(4piepsilon_0)q/((a^2+r^2)) [1+1] a/((a^2+r^2)^(1//2)) -hatP =1/(4piepsilon_0)(2qa)/((a^2+r^2)^(3//2))-hatP`
`vecE=1/(4piepsilon_0)P((a^2+r^2)^(3//2))-hatP` P=q 2a
`vecE=1/(4piepsilon_0)vecP/((a^2+r^2)^(3//2)) " " because hatP=vecP/P`
As a < < < r , a can be neglected
`vecE=1/(4piepsilon_0)vecP/((r^2)^(3//2))`
`vecE=1/(4piepsilon_0)vecP/r^3`