A running track of 440 ft is to be laid out enclosing a football field, the shape of which is a rectangle with a semi-circle at each end. If the area of the rectangular portion is to be maximum, then find the length of its sides.
To solve the problem of maximizing the area of the rectangular portion of a football field enclosed by a running track, we will follow these steps:
Step 1: Understand the Problem
We have a running track with a total perimeter of 440 ft, enclosing a rectangular field with semicircles at each end. We need to find the dimensions of the rectangle that maximize its area.
Step 2: Set Up the Variables
Let:
- x = length of the rectangular portion
- r = radius of the semicircles
Step 3: Write the Perimeter Equation
The total perimeter of the track can be expressed as:
Perimeter=2x+2πr=440
From this, we can simplify to:
x+πr=220(1)
Step 4: Express the Area of the Rectangle
The area A of the rectangular portion can be expressed as:
A=x⋅(2r)=2xr(2)
Step 5: Substitute for r
From equation (1), we can express r in terms of x:
πr=220−x⟹r=220−xπ(3)
Step 6: Substitute r into the Area Formula
Substituting equation (3) into equation (2):
A=2x⋅220−xπ=2x(220−x)π
This simplifies to:
A=440x−2x2π(4)
Step 7: Differentiate the Area Function
To find the maximum area, we differentiate A with respect to x:
dAdx=1π(440−4x)
Step 8: Set the Derivative to Zero
Setting the derivative equal to zero to find critical points:
440−4x=0⟹4x=440⟹x=110(5)
Step 9: Verify Maximum Using Second Derivative Test
Now we check the second derivative:
d2Adx2=ddx(1π(440−4x))=−4π
Since −4π<0, this indicates a maximum at x=110.
Step 10: Find the Radius r
Substituting x=110 back into equation (1) to find r:
110+πr=220⟹πr=110⟹r=110π≈35 ft(6)
Step 11: Determine the Dimensions of the Rectangle
The dimensions of the rectangle are:
- Length =x=110 ft
- Width =2r=2⋅110π≈70 ft
Conclusion
The dimensions of the rectangular portion of the football field that maximize the area are:
- Length = 110 ft
- Width = 70 ft
We have a running track with a total perimeter of 440 ft, enclosing a rectangular field with semicircles at each end. We need to find the dimensions of the rectangle that maximize its area.
Let:
- x = length of the rectangular portion
- r = radius of the semicircles
The total perimeter of the track can be expressed as:
Perimeter=2x+2πr=440
From this, we can simplify to:
x+πr=220(1)
The area A of the rectangular portion can be expressed as:
A=x⋅(2r)=2xr(2)
From equation (1), we can express r in terms of x:
πr=220−x⟹r=220−xπ(3)
Substituting equation (3) into equation (2):
A=2x⋅220−xπ=2x(220−x)π
This simplifies to:
A=440x−2x2π(4)
To find the maximum area, we differentiate A with respect to x:
dAdx=1π(440−4x)
Setting the derivative equal to zero to find critical points:
440−4x=0⟹4x=440⟹x=110(5)
Now we check the second derivative:
d2Adx2=ddx(1π(440−4x))=−4π
Since −4π<0, this indicates a maximum at x=110.
Substituting x=110 back into equation (1) to find r:
110+πr=220⟹πr=110⟹r=110π≈35 ft(6)
The dimensions of the rectangle are:
- Length =x=110 ft
- Width =2r=2⋅110π≈70 ft
The dimensions of the rectangular portion of the football field that maximize the area are:
- Length = 110 ft
- Width = 70 ft
Similar Questions
A running track of 440 ft is to be laid out enclosing a football field, the shape of which is a rectangle with a semi-circle at each end. If the area of the rectangular portion is to be maximum, then find the length of its sides.
View SolutionA field has the shape of a rectangle having a semi-circle at its one end as shown in the figure. Find the area of the field.
View Solution
Knowledge Check
A playground is in the form of a rectangle having semicircle on the shorter sides. Find its area when the length of the rectangular portion is 80 m and the breadth is 42 m.
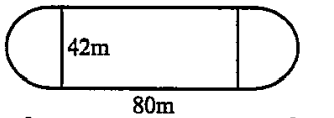 A4746m2B4748m2C4950m2D5049m2
A4746m2B4748m2C4950m2D5049m2Find the radius of the semic-circle.
I. The area of semi-circle is equal to the area of the rectangle.
II. The breadth of rectangle is 5 cm less than its length and its permeter is 50 cm.Aif the data in statement I alone are sufficient to answer the questin, while the data in statement II alone are not sufficient to answer the question.Bif the data in statement II alon are sufficient to answer the question, while the data in statement I alone are not sufficient to answer the question.Cif the data either in statement I alone or in statement II alone in sufficient to answer the question.Dif the data in both the statements I and II together are necessary to answer the question.From four corners of a square sheet of side 4 cm, four pieces, each in the shape of arc of a circle with radius 2 cm, are cut out. The area of the remaining portion is :
A(8−π) sq. mB(16−4π) sq. cmC(16−8π) sq. cmD(4−2π) sq. cm.
A window is in the shape of a rectangle surmounted by a semi circle. If the perimeter of the window is of fixed length then the maximum area of the window is
View SolutionThe inside perimeter of a running track (shown in figure) is 400m. The length of each of the straight portion is 90m and the ends are semi-circles. If the track is everywhere 14m wide, find the area of the track. Also find the length of the outer running track.
View SolutionThe inside perimeter of a running track (shown in figure) is 400m. The length of each of the straight portion is 90m and the ends are semi-circles. If track is everywhere 14m wide, find the area of the track. Also, find the length of the outer running track.
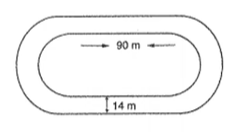
View SolutionA playground has the shape of a rectangle, with two semi-circles on its smaller sides as diameters, added to its outside. If the sides of the rectangle are 36m and 24.5m, find the area of the playground. (Take π=227)
View SolutionThe inner perimeter of a running track (shown in figure) is 400 m. The length of each of the straight portion is 90 m and the ends are semicircular. If the track is everywhere 14 m wide, find the area of the track. Also, find the length of the outer running track.

View Solution
