Show that efficiency of Caront's ideal heat engine is $η = (1 - \frac{T_{2}}{T_{1}})$ .Solution in Kannada

Video Solution

Text Solution

Verified by Experts

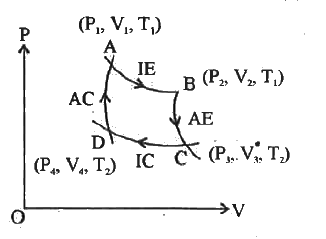
Carnot.s ideal heat engine completes a sequence of isothermal and adiabatic expansion and isothermal and adiabatic compression. The working substance returns to intial state. Heat absorbed by the system from the sourece at $T_{1} K$ is
$W_{1} = Q_{1} = μ R T_{1} {log}_{e} (\frac{V_{2}}{V_{1}}) . ... ... . (1)$
Total work done $W = W_{1} + W_{2} + W_{3} + W_{4}$
Where $W_{1} & W_{3}$ refres to isothermal process and $W_{2} & W_{4}$ refers to adiabatic process.
$W_{2} = \frac{μ R T}{(γ - 1)} (T_{1} - T_{2})$ [adiabatic expansion]
and $W_{4} = \frac{- μ R T}{(γ - 1)} (T_{1} - T_{2})$ [adiabatic compression]
So that $W_{2} + W_{4} = 0$
For an adiabatic expansion,
$(\frac{T_{1}}{T_{2}}) = {(\frac{V_{3}}{V_{2}})}^{γ - 1} ... ... . (2)$
and adiabatic compression,
$(\frac{T_{1}}{T_{2}}) = {(\frac{V_{4}}{V_{1}})}^{γ - 1} ... ... . (3)$
From (2) & (3) $\frac{V_{3}}{V_{2}} = \frac{V_{4}}{V_{1}} or \frac{V_{3}}{V_{4}} = \frac{V_{2}}{V_{1}} ... ... ... ... (4)$
For isothermal expasion and compression, total work done $= W_{1} + W_{3} = μ R T_{1} {log}_{e} (\frac{V_{2}}{V_{1}}) - μ R T_{2} log (\frac{V_{2}}{V_{4}})$ .
Applying (2) & (3) we get $W = μ R (T_{1} - T_{2}) {log}_{e} (\frac{V_{2}}{V_{1}}) ... ... ... ... (5)$
Hence efficiency $η = \frac{W}{Q_{1}} = \frac{(5)}{(1)} = \frac{T_{1} - T_{2}}{T_{1}}$
i.e., $η = 1 - \frac{T_{2}}{T_{1}} also η = 1 - \frac{Q_{2}}{Q_{1}} as T_{2} \propto Q_{2} & T_{1} \propto Q_{1}$ .

Updated on:21/07/2023

|

Class 11 PHYSICS THERMODYNAMICS

Topper's Solved these Questions

Similar Questions

SUBHASH PUBLICATION-THERMODYNAMICS-FIVE MARKS QUESTIONS WITH ANSWERS

Home
Ask Doubt
Profile