Let X denote the sum of the numbers obtained when two fair dice are rolled. Find the variance and standard deviation of X.
The correct Answer is:N/a
Let X repesents the sum of the numbers obtained when two unbiased dice are thrown. Since the sum of two numbers obtained cannot be equal to 1 when two unbiased dice are thrown. Therefore, the values of X can be 2,3,4,5,6,7,8,9,10,11,12.
P(X=2)=P[{1,1}]=136
P(X=3)=P[{(1,2),(2,1)}]=236
P(X=4)=P[{(1,3),(2,2),(3,1)}]=336
P(X=5)=P[{(1,4),(2,3),(3,2),(4,1)}]=436
P(X=6)=P[{(1,5),(2,4),(3,3),(4,2),(5,1)}]
=536
P(X=7)=P[{(1,6),(2,5),(3,4),(4,3),(5,2),(6,1)}]
=636
P(X=8)=P[{(2,6),(3,5),(4,4),(5,3),(6,2)}]
=536
P(X=9)=P[{(3,6),(4,5),(5,4),(6,3)}]=436
P(X=10)=P[{(4,6),(5,5),(6,4)}]=336
P(X=11)=P[{(5,6),(6,5)}]=236
P(X=12)=P[66]=136
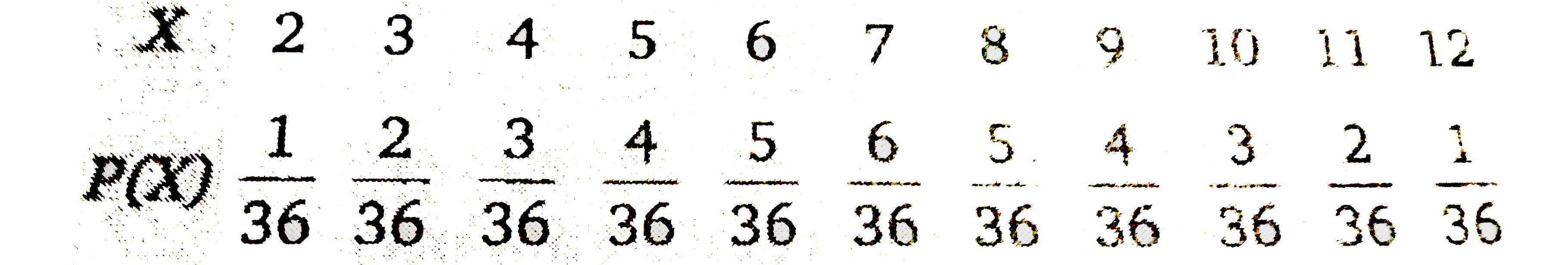
Mean of random variable X
=∑XP(x)
=[2×1+3×2+4×3+5×+6×5+7×6+8×5+9×4+10×3+11×2+12×1]36
=[2+6+12+20+30+42+40+36+30+22+12]36=25236=7
Variance of random variable X=∑X2P(X)−(mean)2
=[22×1+32×2+42×3+52×4+62×5+72×6+82×5+92×4+102×3+112×2+122×1]36−72
=[4+18+48+100+180+294+320+324+300+242+144]36
=197436−49=1974−176436=21036=356
Therefoe, standard deviation,
SD=√variance=√356=√5.833=2.415
Topper's Solved these Questions
- PROBABIILITYBook:NAGEEN PRAKASHANChapter:PROBABIILITYExercise:Exercise 13.5
Explore 15 Videos
- PROBABIILITYBook:NAGEEN PRAKASHANChapter:PROBABIILITYExercise:Miscellaneous Exercise
Explore 19 Videos
- PROBABIILITYBook:NAGEEN PRAKASHANChapter:PROBABIILITYExercise:Exercise 13.3
Explore 14 Videos
- MATRICESBook:NAGEEN PRAKASHANChapter:MATRICESExercise:Miscellaneous Exerice
Explore 15 Videos
- RELATIONS AND FUNCTIONS Book:NAGEEN PRAKASHANChapter:RELATIONS AND FUNCTIONS Exercise:Miscellaneous Exercise
Explore 19 Videos
Similar Questions
Knowledge Check
If X denotes the sum of the numbers obtained when two fair dice are rolled, then the variance and standard deviation of X are
A316 and √316B356and√356C176 and √176D316 and √356The expected value of the sum of the two numbers obtained when two fair dice are rolled is
A7B14C203D509
Two numbers are selected at random (without replacement) from first six positive integers. Let X denote the larger of the two numbers obtained. Find the probability distribution of X. Find the mean and variance of this distribution.
View SolutionThere are 4 cards numbered 1, 3, 5 and 7, one number on one card. Two cards are drawn at random without replacement. Let 'X' denote the sum of the numbers on the two drawn cards. Find the mean and variance of X.
View SolutionThere are 5 cards numbered 1 to 5 , one number on one number on one card . Two cards are drawn at random without replacement . Let X denotes the sum of the numbers on two cards drawn . Find the mean and variance of X.
View SolutionTwo numbers are selected at random (without replacement) from positive integers 2,3,4,5,6, and 7 . Let X denote the larger of the two numbers obtained. Find the mean and variance of the probability distribution of X .
View SolutionTwo numbers are selected are random (without replacement) from positive integers 2, 3, 4, 5, 6 and 7. Let X denote the larger of the two numbers obtained. Find the mean and variance of the probability distribution of X.
View SolutionFind the mean, variance and standard deviation of first n natural numbers.
View Solution