A man wishes to mix two types of food X and Y in such a way that the vitamins contents of the mixture contain at least B units of vitamin A and 11 units of vitamin B. Food X costs Rs. 50 per kg and food Y costs Rs. 60 per kg. Fod Xcontains 2 units per kg of vitamin A and 5 kg per unit of vitamin B while food Y contains 5 units per kg of vitamin A and 2 units per kg of vitamin B. Determine the minimum cost of the mixture.
Let there is x kg of food X and y kg of food Y in the mixture.
∴ Minimize cost z=50x+60y
Subject to x≥0
y≥0
2x+5y≥8 brgt 5x+2y≥11
Draw the graph of equations x=0,y=0,2x+4y=8 and 5x+2y=11.
Now the feasible region for the inequations x≥0,y≥0,2x+5y≥8,5x+2y≥11, and shade it. The vertices of the shaded region are A(4,0),B(0,112) and C(137,67). We will find the value of z at these vertices.
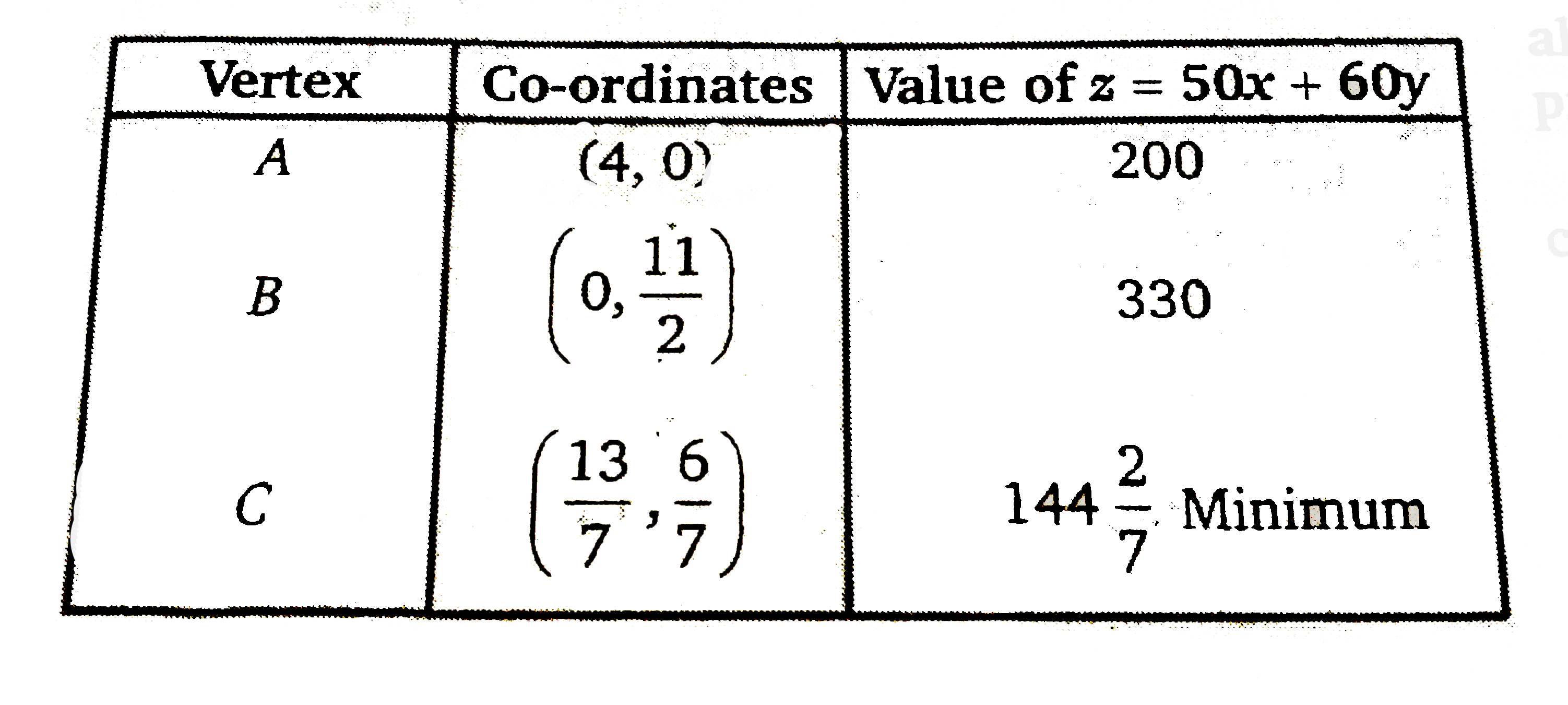

Therefore the minimum cost is Rs. 14427 and food X and Y are taken 137 kg and 67 respectively.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - LINEAR PROGRAMMINGEXERCISE - Exercise 12 A8videos
LINEAR PROGRAMMING
- BOOK - NAGEEN PRAKASHANCHAPTER - LINEAR PROGRAMMINGEXERCISE - Exercise 12 B17videos
LINEAR PROGRAMMING
- BOOK - NAGEEN PRAKASHANCHAPTER - INVERES TRIGONOMETRIC FUNCTIONSEXERCISE - Miscellaneous Exercise (prove That )9videos
INVERES TRIGONOMETRIC FUNCTIONS
- BOOK - NAGEEN PRAKASHANCHAPTER - MATRICESEXERCISE - Miscellaneous Exerice15videos
MATRICES
Similar Questions
Reshma wishes to mix two types of food P and Q in such a way that the vitamin contents of the mixture contain at least 8 units of vitamin A and 11 units of vitamin B. Food P costs Rs 60 / kg and Food Q costs Rs 80 / kg. Food P contains 3 units/kg of Vitamin A and 5 units / kg of Vitamin B while food Q contains 4 units kg of Vitamin A and 2 units/kg of vitamin B. Determine the minimum cost of the mixture.
View SolutionReshma wishes to mix two types of food P and Q in such a way that the vitamin contents of the mixture contain at least 8 units of vitamin A and 11 units of vitamin B. Food P costs Rs 60 / kg and Food Q costs Rs 80 / kg. Food P contains 3 units/kg of Vitamin A and 5 units / kg of Vitamin B while food Q contains 4 units "kg of Vitamin A and 2 units/kg of vitamin B. Determine the minimum cost of the mixture.
View SolutionReshma wishes to mix two types of food P and Q in such a way that the vitamin contents of the mixture contain at leat 8 units of vitamin A and 11 units of vitamin B. Food P cost Rs. 60/kg and Food Q costs Rs. 80/kg. Food P contains 3 units/kg of vitamin A and 5 units/kg of Vitamin B while food Q contains 4 units/kg of vitamin A and 2 units/kg of vitamin B. Determine the minimum cost of the mixture.
View SolutionA woman wishes to mix two types of food in such a way that the vitamin contents of the mixture contain at least 8 units of vitamin A and 11 units of vitamin B. Food I costs Rs.60/kg and food of vitamin B. Food II cost Rs. 80/kg. Food I contains 3 units/kg of vitamin A and 5 units/kg of vitamin B while food II contains 4 units/kg of vitamin A and 2 units/kg of vitamin B. Find the minimum cost of the mixture.
View SolutionA dietician wishes to mix two types of food in such a way that the vitamin contents of the mixture contain at least 8 units of vitamin A and 10 units of vitamin C . Food I contains 2 units per kg of vitamin A and 1 unit per kg of vitamin C , while food II contains 1 unit per kg of vitamin A and 2 units per kg of vitamin C . It costs Rs 5 per kg to purchase food I and Rs 7 per kg to purchase food II . Identify the objective function so as to minimize the cost of mixture.
View SolutionA dietician wishes to mix two types of foods in such a way that the vitamin contents of the mixture contains at least 8 units of vitamin A and 10 units of vitamin C. Food I contains 2 units/kg of vitamin A and 1 units/kg of vitamin C while Food II contains 1 unit/kg of vitamin A and 2 units/kg of vitamin C. It costs Rs.5 per kg to purchase Food I and Rs.7 per kg to purchase Food II. Determine the minimum cost of such a mixture. Formulate the above as a LPP and solve it graphically.
View SolutionA dietician wishes to mix two types of foods in such a way that the vitamin contents of the mixture contains at least 8 units of vitamin A and 10 units of vitamin C. Food I contains 2 units/kg of vitamin A and 1 units/kg of vitamin C while Food II contains 1 unit/kg of vitamin A and 2 units/kg of vitamin C. It costs Rs.5 per kg to purchase Food I and Rs.7 per kg to purchase Food II. Determine the minimum cost of such a mixture. Formulate the above as a LPP and solve it graphically.
View SolutionA dietician wishes to mix two types of food in such a way that the vitamin contents of the mixture contain at least 8 units of Vitamin A and 10 units of vitamin C, Food I contains 2 units per kg of vitamin A and 1 unit per kg of vitamin C while food II contains 1 unit per kg of vitamin A and 2 units per kg of vitamin C. It costs Rs 50.00 per kg to purchase food I and Rs. 70.00 per kg to produce food II. Formulate the above linear programming problem to minimize the minimize the cost of such a mixture.
View SolutionA dietician wishes to mix two types of food in such a way that the vitamin contents of the mixture contain at least 8 units f Vitamin A and 10 units of vitamin C, Food ‘I’ contains 2 units per kg of vitamin A and 1 unit per kg of vitamin C while food ‘II’ contains 1 unit per kg of vitamin A and 2 units per kg of vitamin C. It costs Rs 50.00 per kg to purchase food ‘I’ and Rs. 70.00 per kg to produce food ‘II’. Formulate the above linear programming problem to minimize the minimize the cost of such a mixture.
View SolutionA dietician wishes to mix two types of food in such a way that the vitamin contents of the mixture contain at least 8 units of vitamin A and 10 units of vitamin C. Foot ‘I’ contain 2 units/kg of vitamin A and 1 unit/kg of vitamin C while food ‘II’ contain 1 unit/kg of vitamin A and 2 units/kg of vitamin C. it costs Rs. 5.00 per kg to purchase food ‘I’ and Rs. 7.000 per kg to produce food ‘II’. Determine the minimum cost to such a mixture. Formulate the above as a LPP and solve it.
View Solution
