Using integration find the area of region bounded by the triangle whose vertices are $(1, 0), (1, 3) a n d (3, 2)$ .

Video Solution

Text Solution

Verified by Experts

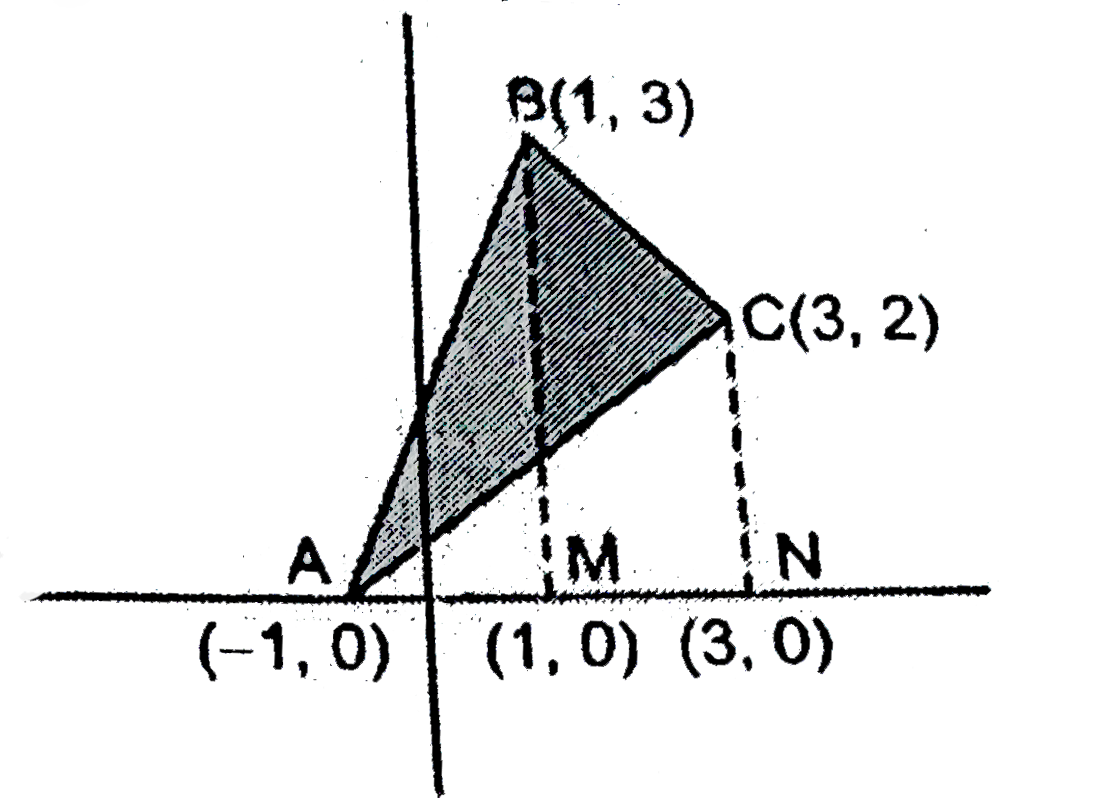
Let the given three points be A (-1, 0), B(1, 3) and C(2, 2).
We know that the equation of a line passing through the points $(x_{1}, y_{1})$ and $(x_{2}, y_{2})$ is
$(y - y_{1}) = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} (x - x_{1}) .$
$∴$ Equation of line AB,
$y - 0 = \frac{3 - 0}{1 + 1} (x + 1) \Rightarrow y = \frac{3}{2} (x + 1)$
Equation of line BC,
$y - 3 = \frac{2 - 3}{3 - 1} (x - 1)$
$\Rightarrow y = - \frac{1}{2} x + \frac{1}{2} + 3 \Rightarrow y = - \frac{1}{2} x + \frac{7}{2}$
and equation of line AC,
$y - 0 = \frac{2 - 0}{3 + 1} (x + 1) \Rightarrow y = \frac{1}{2} x + \frac{1}{2}$
$a r (△ A B C) = a r (△ A M B) + a r (□ B M N C) - a r (△ A N C)$
$= \int_{- 1}^{1} \frac{3}{2} (x + 1) d x + \int_{1}^{3} (- \frac{1}{2} x + \frac{7}{2}) d x - \int_{- 1}^{3} (\frac{1}{2} x + \frac{1}{2}) d x$
$= \frac{3}{2} {[\frac{x^{2}}{2} + x]}_{- 1}^{1} + {[- \frac{x^{2}}{4} + \frac{7}{2} x]}_{1}^{3} - {[\frac{x^{2}}{4} + \frac{1}{2} x]}_{- 1}^{3}$
$= \frac{3}{2} [\frac{1}{2} + 1 - \frac{1}{2} - (- 1)] + (- \frac{9}{4} + \frac{21}{2} + \frac{1}{4} - \frac{7}{2}) - (\frac{9}{4} + \frac{3}{2} - \frac{1}{4} + \frac{1}{2})$
$= \frac{3}{2} (2) + (7 - 2) - (2 + 2)$
$= 3 + 5 - 4 = 4$ sq. units.

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Orthocentre of the triangle whose vertices are (1, 1) (3, 5) and (3, 0), is
A $(- 1, 1)$
B $(1, - 1)$
C(1, 1)
DNone of these

NAGEEN PRAKASHAN-APPLICATIONS OF INTEGRALS-Exercise 8.2

Home
Ask Doubt
Profile