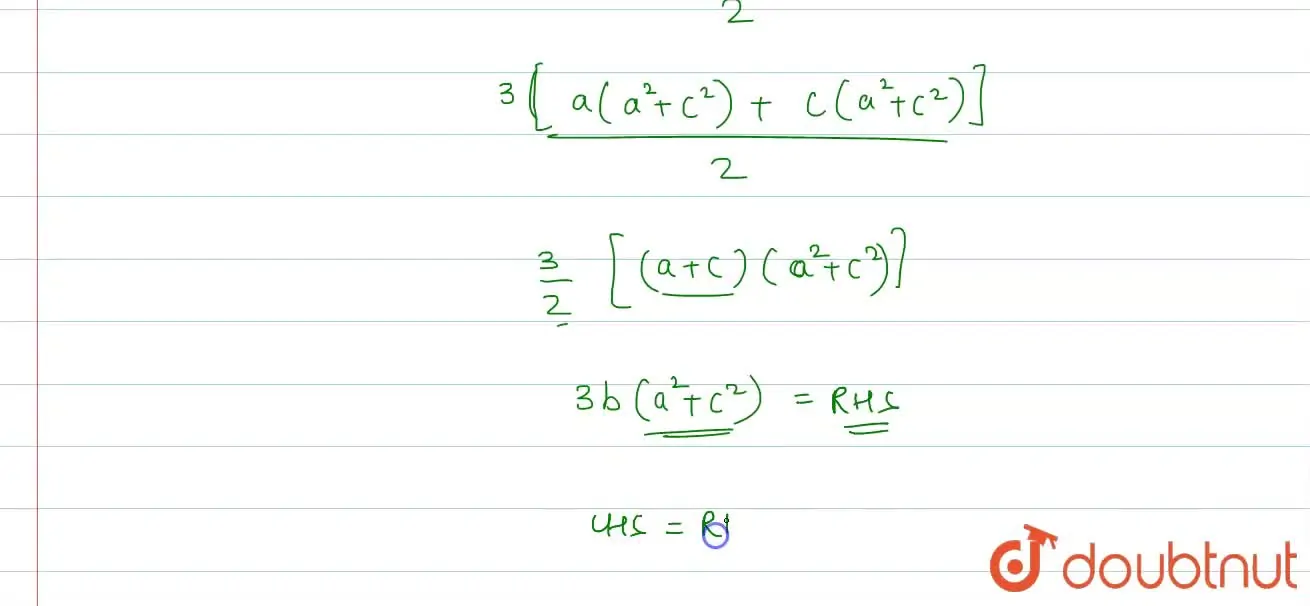If a, b, c are in A.P., prove that a3+4b3+c3=3b(a2+c2).
The correct Answer is:N/a
If a, b, c are in A.P.
∴ b=a+c2
L.H.S.=a3+4b3+c3
=a3+4(a+c2)+c3
=a3+4(a3+3a2c+3ac2+c3)8+c3
=2a3+a3+3a2c+3ac2+c3+2c32
=3a3++3a2c+3ac2+3c32
=3(a3+a2c+ac2+c3)2
=3(a+c)(a2+c2)2
=3b(a2+c2) [From eq. (1)]
=R.H.S.
Related Playlists
- BOOK - NAGEEN PRAKASHANCHAPTER - SEQUENCE AND SERIESEXERCISE - Exercise 9A4videos
SEQUENCE AND SERIES
- BOOK - NAGEEN PRAKASHANCHAPTER - SEQUENCE AND SERIESEXERCISE - Exercise 9B17videos
SEQUENCE AND SERIES
- BOOK - NAGEEN PRAKASHANCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - MISCELLANEOUS EXERCISE12videos
RELATIONS AND FUNCTIONS
- BOOK - NAGEEN PRAKASHANCHAPTER - SETSEXERCISE - MISC Exercise16videos
SETS
Similar Questions
If a,b,c, are in AP, prove that a3+4b3+c3=3b(a2+c2)
View SolutionIf a,b,c are in A.P., prove that 8b3−a3−c3=3ac(a+c)
View SolutionIf a,b,c are in A.P. prove that (a−c)2=4(a−b)(b−c)
View SolutionIf a, b, c are in A.P., prove that a2(b+c),b2(c+a),c2(a+b) are also in A.P.
View SolutionIf a,b,c are in A.P., prove that a2+c2−2bc=2a(b−c).
View SolutionIf a,b,c are in G.P., prove that: 1) a(b2+c2)=c(a2+b2)
, 2) A2b2c2(1a3+1b3+1c3)=a3+b3+c3
, 3) (a+b+c)2a2+b2+c2=a+b+ca−b+c
, 4)1a2−b2+1b2=1b2−c2
,5) (a+2b=2c)(a−2b+2c)=a2+4c2.View SolutionIf a,b,c are in A.P., prove that: i.(a−c)2=4(a−b)(b−c)
ii.a2+c2+4ac=2(ab+bc+ca)
iii.a3+c3+6abc=8b3View SolutionIf a,b,c are in A.P., then prove that: (a−c)2=4(b2−ac), a3+4b3+c3=3b(a2+c2)
View Solutionif a,b,c are in AP, prove that (a−c)2=4(b2−ac)
View SolutionIf a, b, c are in A.P, show that(i)a3+b3+6abc=8b3 (ii) (a+2b−c)(2b+c−a)(a+c−b)=4abc
View Solution