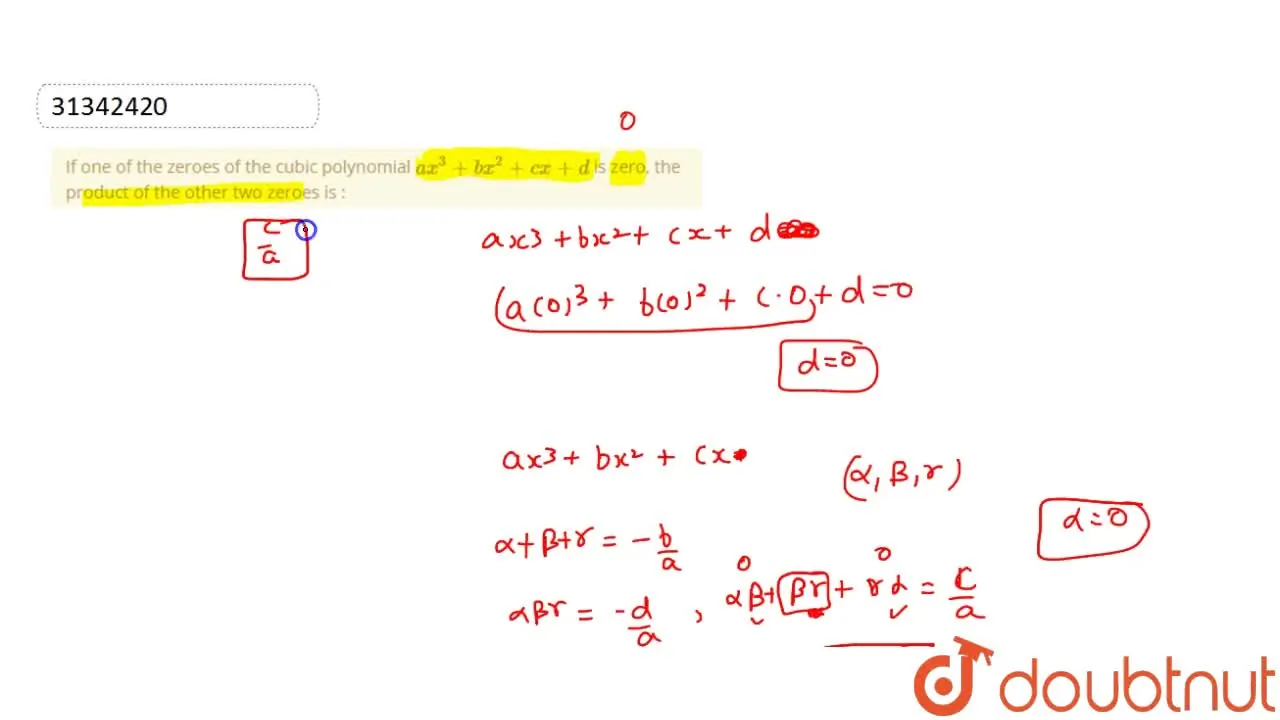
If one of the zeroes of the cubic polynomial ax^(3)+bx^(2)+cx+d is zer

Given that one of the zereos of the cubic polynomial $a x^{3} + b x^{2} + c x + d$ is zero ,the product of the other two zeroes is
A $- \frac{c}{a}$
B $\frac{c}{a}$
C0
D $- \frac{b}{a}$
If one of the zereos of the cubic polynomial $x^{3} + a x^{2} + b x + c$ is -1, then the product of the other two zeroes is
A $b - a + 1$
B $b - a - 1$
C $a - b + 1$
D $a - b - 1$
If one of the zeroes of the cubic polynomial $x^{3} + a x^{2} + b x + c$ is -1, then the perpendicular of the other two zeroes is
A $b - a + 1$
B $b - a - 1$
C $a - b + 1$
D $a - b - 1$

If one of the zeroes of the cubic polynomial $a x^{3} + b x^{2} + c x + d$ is zero, the product of the other two zeroes is :