In a trapezium ABCD, AB || DC, AB = a cm, and DC = b cm. If M and N are the midpoints of the nonparallel sides, AD and BC respectively then find the ratio of ar(DCNM) and ar(MNBA).
The correct Answer is:(3a+b):(a+3b)
Step by step video, text & image solution for In a trapezium ABCD, AB || DC, AB = a cm, and DC = b cm. If M and N are the midpoints of the nonparallel sides, AD and BC respectively then find the ratio of ar(DCNM) and ar(MNBA). by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (very Short Answer Questions)
10 Videos
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Revision Exercise (long Answer Questions )
5 Videos
Similar Questions
Knowledge Check
In figure, if DE||BC, then find the ratio of ar (ΔADE) and ar(DECB).
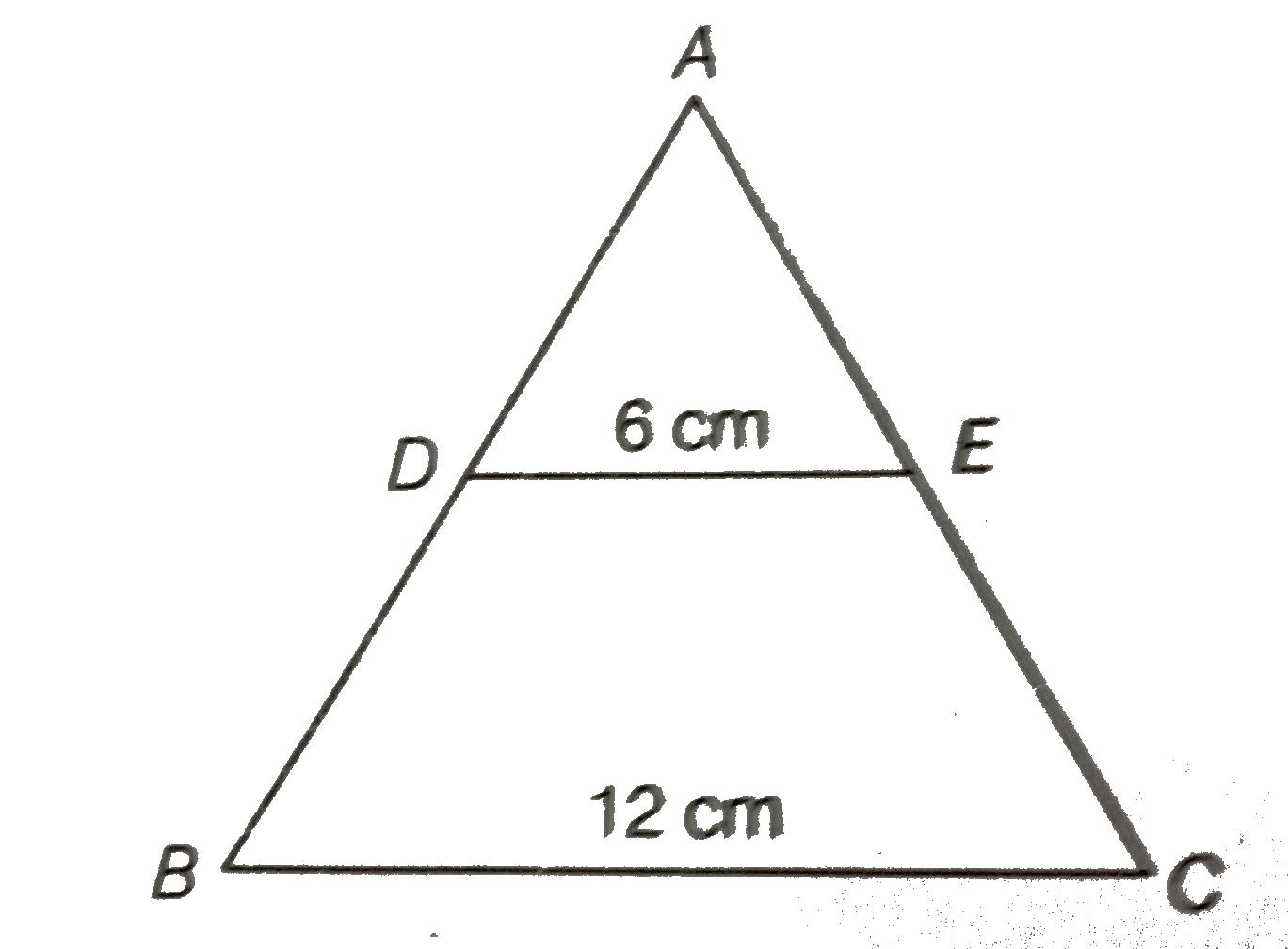 A1:3B1:2C2:5D3:5
A1:3B1:2C2:5D3:5ABCD is a trapezium in which AB || DC a and DC= 40 cm and AB = 60 cm. If X and Y a re respectively, the midpoints of AD and BC, then

XY=A40 cmB50 cmC60 cmD30 cmIn a trapezium ABCD, AB||DC, AB = AD, ∠ADC=64∘and∠BCD=54∘. Find ∠DBC.
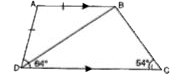 A64∘B72∘C94∘D116∘
A64∘B72∘C94∘D116∘
ABCD is a trapezium with AB || DC. E and F are points on non-parallel sides AD and BC respectively such that EF is parallel to AB. Show thatAEED=BFFC.
View SolutionABCD is a trapezium in which AB || DC, AB = 16 cm and DC = 24 cm. If E and Fare respectively the midpoints of AD and BC, prove that ar(ABFE) = 911 ar(EFCD).
View SolutionABCD is trapezium in which AB∣∣DC, DC = 30 cm and AB = 50 cm. If X and Y are, respectively the mid-points of AD and BC, prove that
ar(DCYX)=79ar(XYBA).
View SolutionIn a trapezium ABCD, DC || AB , AB = 12 cm and DC = 7.2 cm. What is the length of the line segment joining the mid- points of its diagonals?
View SolutionP and Q are any two points lying on the sides DC and AD respectively of a parallelogramABCD. Show that ar (APB) = ar (BQC).
View Solution
