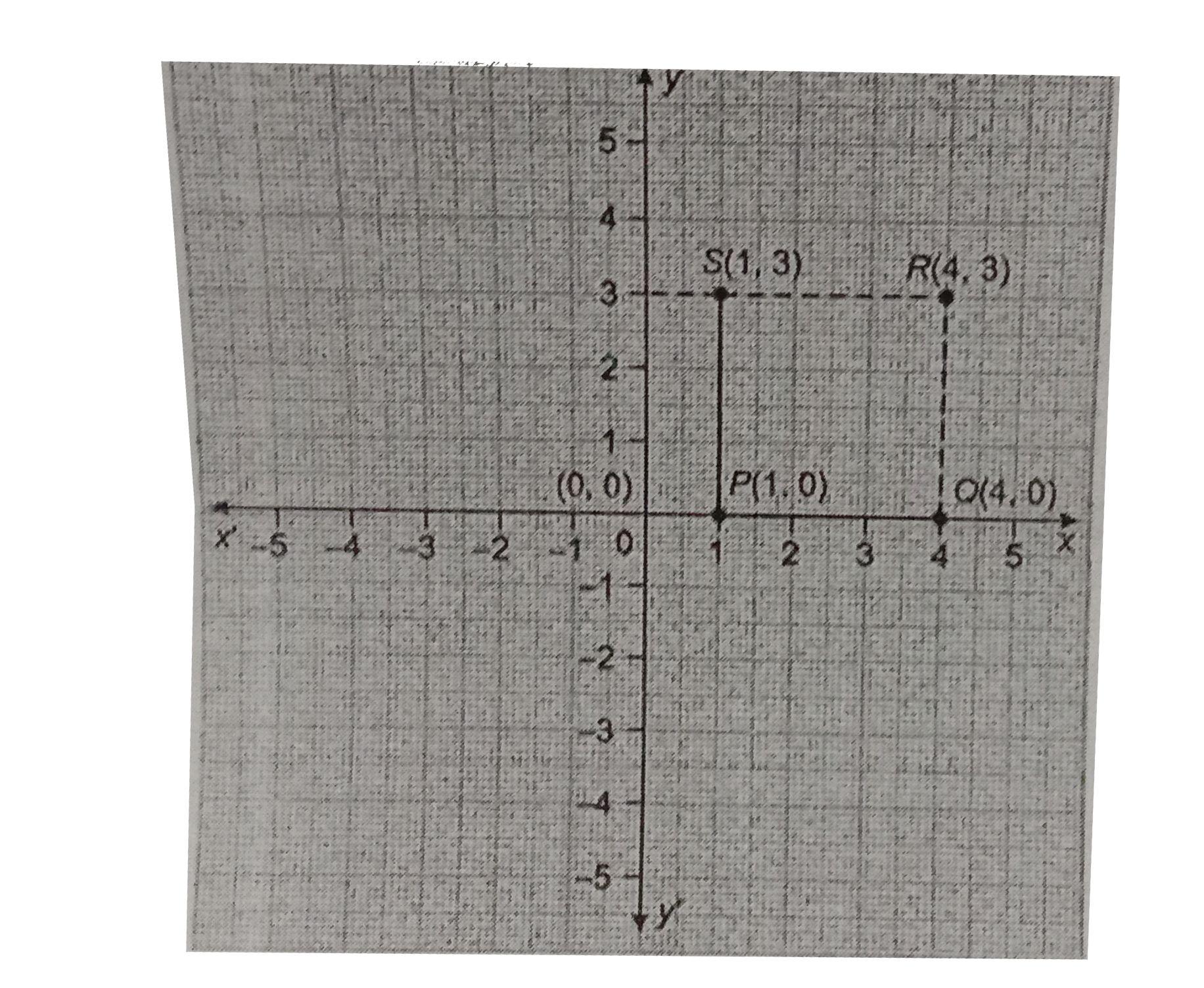
Plot point $P (1, 0), Q (4, 0) and S (1, 3)$ . Find the coordinates of $R$ so that $P Q R S$ is a square.

Video Solution

Text Solution

Verified by Experts

Plot the points $P (1, 0), Q (4, 0) and S (1, 3)$ in the cartesian, As we known all the sides of a square ar equal and each angle is of $90^{\circ}$ measure. Therefore, the abscissa of the vertex R is 4 and its ordinate is 3.

Updated on:21/07/2023

Plot the points P(1, 0), Q(4,0) and S(1, 3). Find the coordinates of the point R such that PQRS is a square.
A(2,3)
B(3,3)
C(4,3)
D(0,3)
A point E with x-coordinate 4 lies on the line segment joining the point P $(2, - 3, 4)$ and Q(8,0,10). Find the coordinates of the point R
A $(4, - 2, - 6)$
B(4, 2, 6)
C $(4, - 2, 6)$
DNone of the these
If the points P(a, -11), Q(5, b), R(2, 15) and S(1, 1) are the vertices of a parallelogram PQRS, find the values of a.
A5
B3
C4
D2