Potential energy (PEn) and kinetic energy (KEn) of electron in nth orbit are related as
PEn=KEn
PEn=−2KEn
PEn=2KEn
PEn=KEn
The correct Answer is:B
To find the relationship between the potential energy (PE) and kinetic energy (KE) of an electron in the nth orbit, we can follow these steps:
Step 1: Understand the definitions of KE and PE
- The kinetic energy (KE) of an electron in the nth orbit is given by the formula:
KEn=Ze28πϵ0rn
- The potential energy (PE) of the electron in the nth orbit is given by:
PEn=−Ze24πϵ0rn
Step 2: Write the total energy (E) of the electron
- The total energy (E) of the electron in the nth orbit is the sum of its kinetic and potential energy:
En=KEn+PEn
- Substituting the expressions for KE and PE, we get:
En=Ze28πϵ0rn−Ze24πϵ0rn
Step 3: Simplify the total energy expression
- To combine the terms, we need a common denominator:
En=Ze28πϵ0rn−2Ze28πϵ0rn
- This simplifies to:
En=−Ze28πϵ0rn
Step 4: Relate PE and KE
- From the expressions for KE and PE, we can derive the relationship between them:
- We have:
PEn=−Ze24πϵ0rn
and
KEn=Ze28πϵ0rn
- Now, we can express PE in terms of KE:
PEn=−2×KEn
Conclusion
Thus, the relationship between the potential energy and kinetic energy of an electron in the nth orbit is:
PEn=−2×KEn
- The kinetic energy (KE) of an electron in the nth orbit is given by the formula:
KEn=Ze28πϵ0rn
- The potential energy (PE) of the electron in the nth orbit is given by:
PEn=−Ze24πϵ0rn
- The total energy (E) of the electron in the nth orbit is the sum of its kinetic and potential energy:
En=KEn+PEn
- Substituting the expressions for KE and PE, we get:
En=Ze28πϵ0rn−Ze24πϵ0rn
- To combine the terms, we need a common denominator:
En=Ze28πϵ0rn−2Ze28πϵ0rn
- This simplifies to:
En=−Ze28πϵ0rn
- From the expressions for KE and PE, we can derive the relationship between them:
- We have:
PEn=−Ze24πϵ0rn
and
KEn=Ze28πϵ0rn
- Now, we can express PE in terms of KE:
PEn=−2×KEn
Thus, the relationship between the potential energy and kinetic energy of an electron in the nth orbit is:
PEn=−2×KEn
Topper's Solved these Questions
- ATOMSBOOK - DC PANDEYCHAPTER - ATOMSEXERCISE - Check point 12.3
15 Videos
- ATOMSBOOK - DC PANDEYCHAPTER - ATOMSEXERCISE - Taking it together
117 Videos
- ATOMSBOOK - DC PANDEYCHAPTER - ATOMSEXERCISE - Check point 12.1
14 Videos
- ALTERNATING CURRENTBOOK - DC PANDEYCHAPTER - ALTERNATING CURRENTEXERCISE - JEE MAIN
63 Videos
- CAPACITORSBOOK - DC PANDEYCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
Similar Questions
Knowledge Check
Kinetic energy of electron in nth orbit is given by
ARhc2n2B2RhcnCRhcnDRhcn2The energy of the electron in Bohr's orbit related to n as
AE∝1/nBE∝1/n2CE∝nDE∝n2The energy of an electron in nth orbit of hydrogen atom is
A13.6n4eVB13.6n3eVC13.6n2eVD13.6n eV
Derive an expression for the potential energy and kinetic energy of an electron in any orbit of a hydrogen atom, according to Bohr's atomic model. How does P.E. change with increasing n?
View SolutionEnergy Of Electron In Nth Orbit
View Solutionrn,z= Radius of nth orbit of a single electron species having atomic number 'z'
un,z= Velocity of electron in nth orbit of a single electron specie having atomic number 'z'
En,z= Magnitude of total energy of electron in nth orbit of a single electron species having atomic number 'z'.
Kn,z= Magnitude of kinetic energy of electron in nth orbit of a single electron species having atomic number 'z'
Pn,z= Magnitude of potential energy of electron in nth orbit of a single electron species having atomic number 'z'
fn,z= Frequency of electron in nth orbit of a single electron species having atomic number 'z'.
Tn,z= Time period of electron in nth orbit of a single electron species having atomic number 'z'
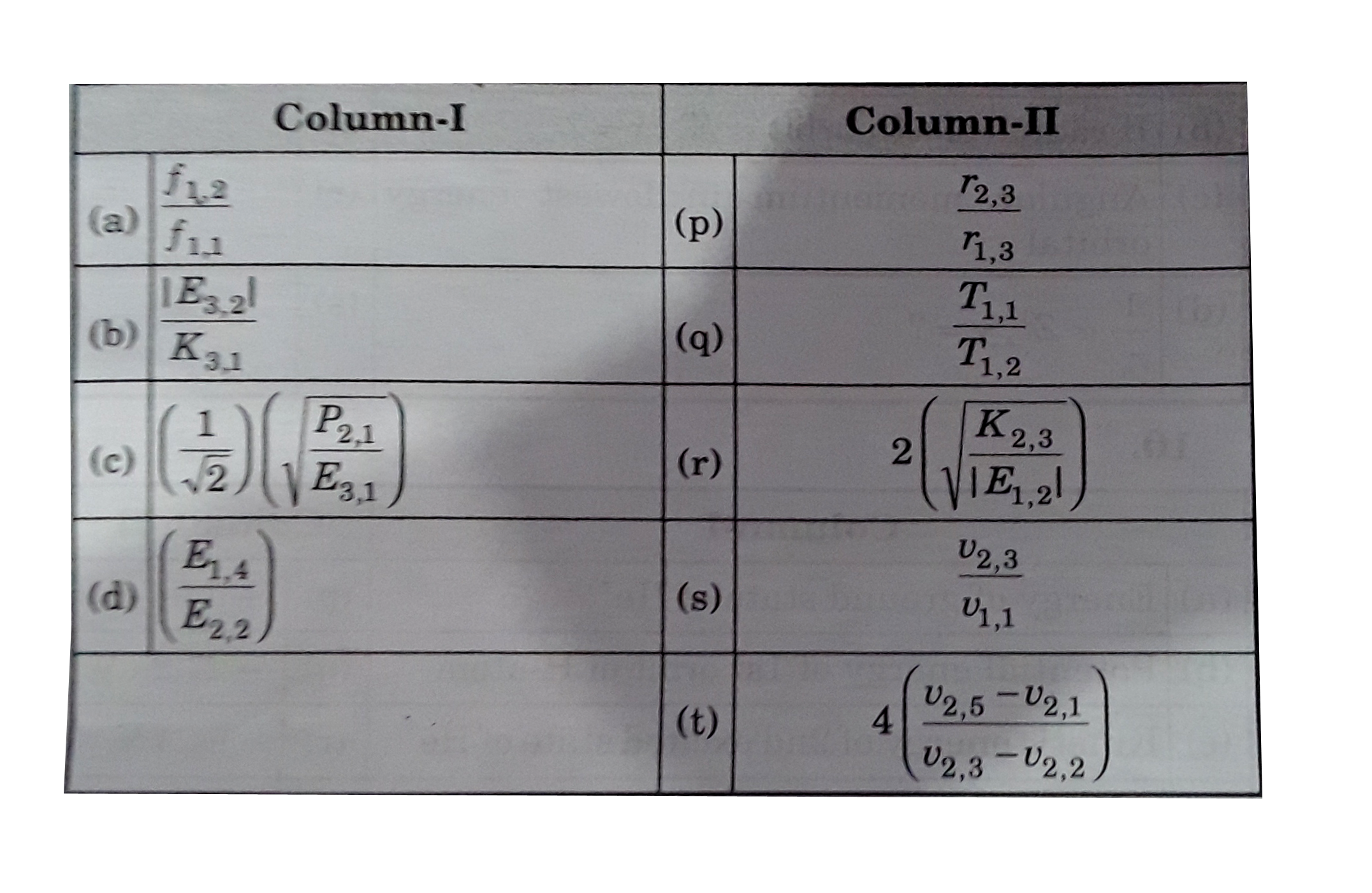
View SolutionWhich of the following option(s) is/are independent of both n and Z for H−like species?
Un= Potential energy of electron in nth orbit
KEn= Kinetic energy of electron in nth orbit
ln= Angular momentam of electoron in nth orbit
vn= Velcity of electron in nth orbit
fn= Frequency of electron in nth orbit
Tn= Time period of revolution of electron in nth orbit
View SolutionThe relationship between kinetic energy (K) and potential energy (U) of electron moving in a orbit around the nucleus is
View Solution
