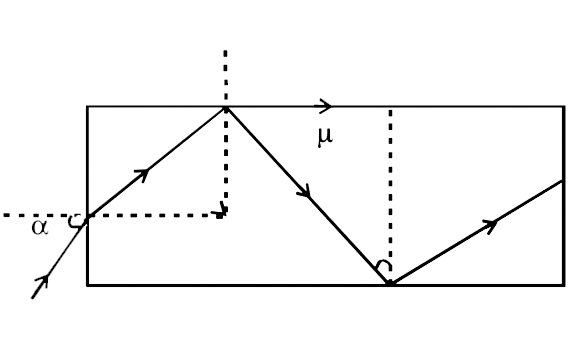
Light enters at an angle of incidence in a transparent rod of refractive index n. For what value of the refractive index of the material of the rod the light once entered into it will not leave it through its lateral face whatsoever be the value of angle of incidence.

Video Solution

Text Solution

Verified by Experts

Let a light ray enters at A and refrected beam is AB. At the lateral face, the angle of incidence is $θ$ . For no refraction at this face, $θ > C$ .
i.e., $sin θ > sin C$
But $θ + r = 90^{\circ} \Rightarrow θ = 90^{\circ} - r$

$sin (90^{\circ} - r) > sin C or cos r > sin C$ .....(i)
By Snell's law, $μ = \frac{sin i}{sin r} \Rightarrow sin r = \frac{sin i}{μ}$
$cos r = \sqrt{1 - {sin}^{2} r} = \sqrt{(1 - \frac{{sin}^{2} i}{n^{2}})}$
From Eq. (i), $\sqrt{1 - \frac{{sin}^{2} i}{n^{2}}} > sin C$
Also, sin C = $\frac{1}{µ} \Rightarrow 1 - \frac{{sin}^{2} i}{n^{2}} > \frac{1}{μ^{2}} or μ^{2} > {sin}^{2} i + 1$
The maximum value of sin i is l.
$μ^{2} > 2 or μ > \sqrt{2}$

Updated on:21/07/2023

Light enters at an angle of incidance in a tranjsparent road of refractve index $μ .$ for what value of the refractive index of the material of the rod the light once entered into it will not leave it through its lateral face whatsoever be the value of angle of incidance ?
A $μ > \sqrt{2}$
B $μ = 1$
C $μ = 1.1$
D $μ = 1.3$
A ray of light is incident at an angle of incidence $45^{\circ}$ on an equilateral prism and emerge at an angle $45^{\circ}$ then the refractive index of the medium of the prism is:
A2
B $\sqrt{2}$
C $\frac{1}{\sqrt{2}}$
D $\sqrt{3}$
A ray of light is incident at an angle of $60^{\circ}$ on the face of a prism with an angle of $60^{\circ}$ . Then the refractive index of the material of the prism is (the prism is in minimum deviation position)
A1.414
B1.623
C1.524
D1.732