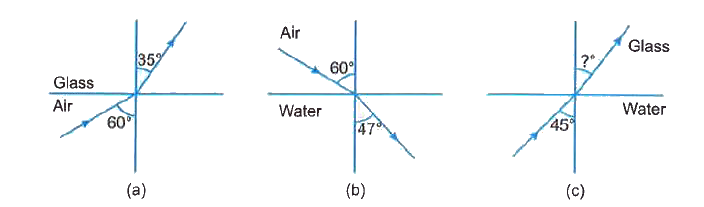
Fig. (a) and (b) show refraction of an incident ray in air at 60∘ with the normal to a glass-air and water-air interface respectively. Predict the angle of refraction of an incident ray in water at 45∘ with the normal to a water glass interface. Take .aμg=1.32.
 .
.
From Fig. (a)
i=angle of incidence=60∘
r= angle of refraction=35∘
∴ Refractive index of glass with repect to water,
aμg=sinisinr=sin60∘sin35∘=0.86600.5736=1.51
From Fig. (b), here, i=60∘ and r=47∘
∴ Refractive index of water with respect to air,
aμw=sinisinr=sin60∘sin47∘=0.86600.7314=1.18
∴ we have aμg=aμw×wμg
or wμg=aμgaμw=1.511.81=1.28
From Fig.(c ), i=angle of incidence=45∘
∴ Using the relation
wμg=sinisinror1.28=sin45∘sinr
or sinr=sin45∘1.28=1/√21.28
=0.7071.28=0.5525=sin33.54'
∴ Angle of refraction,r=33.54∘
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.1
10 Videos
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.2
10 Videos
- NUCLEIBOOK - DC PANDEYCHAPTER - NUCLEIEXERCISE - C MADICAL ENTRANCES GALLERY
46 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
Similar Questions
Fig. 9.02(a) and (b), show refraction of a ray in air incident at 60∘ with the normal to a glass - air and water - air interface, respectively. Predict the angle of refraction in glass when the angle of incidence in water is 45∘ with the normal to a water - glass interface [Fig. 9.02(c)].
View SolutionIf the polarising angle for air glass interface is 56.3∘, what is the angle of refraction in glass ?
View Solution
Knowledge Check
If a ray of light propagating in air strikes a glass slab at an angle of 60∘ with the surface of the slab, the angle of refraction is …......................
Amore than 30∘Bless than 30∘C60∘D30∘The refractive indices of glass and water with respect to air 12and1√3 respectively. Then the refractive index of are glass with respect to water is
A1√3B√32C2√3D2A ray of light travels from air to glass . It is found that the angle of refraction is half the angle of incidence . Then the angle of refraction is given by
Ar=cos−1(n2)Br=sin−1(n2)Cr=tan−1(n2)Dr=cos−1(2n)
If the polarising angle for air glass interface is 56.3∘, what is the angle of refraction in glass ?
View SolutionA light ray falls on the air glass interface at an angle of 30∘. What is the angle of refraction for this rays ? (nag=32).
View SolutionThe refractive index of water and glass with respect to air is 1.3 and 1.5 respectively. Then, the refractive index of glass with respect to water is
View SolutionThe refractive index of glass with respect to air is 32 and the refraction index of water with respect to air is 43. The refractive index of glass with respect to water will be:
View SolutionA ray of light travels from air to glass. It is found that the angle of refraction is half the angle of incidence. The the angle of incidence is given by
View Solution
