The series and parallel circuits shown in figure have the same impedance and the same power factor. If R=3ΩandX=4Ω, find the values of R1andX1. Also, find the impedance and power factor.
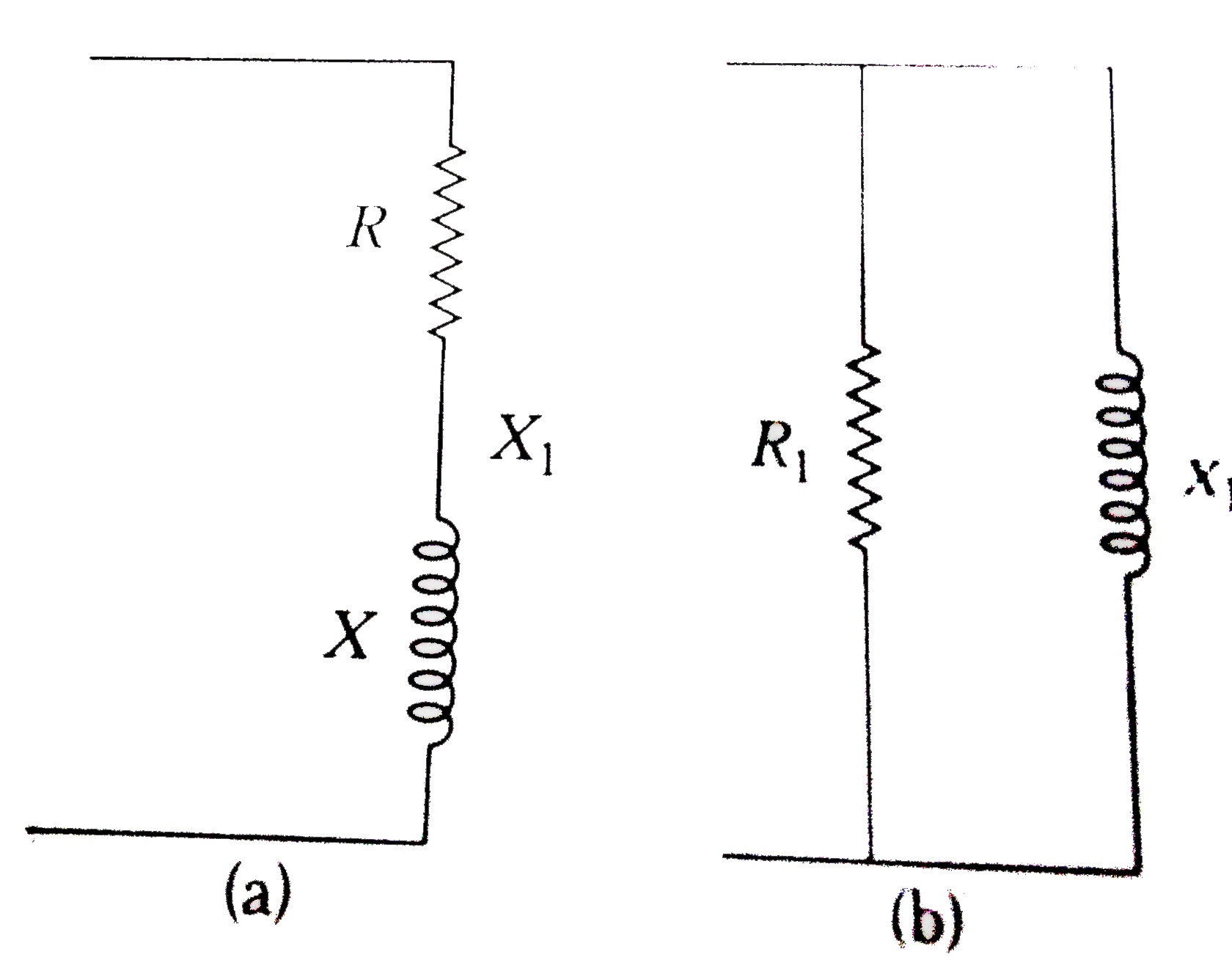
Video Solution
Text Solution

Impedance, Z=√R2+X2=5Ω
Power factor, cosϕ=RZ=35⇒ϕ=cos−1(0,6)
⇒tanϕ=XR=43

Now, we have, (IR)L=V0R1,(IX1)0=V0X1
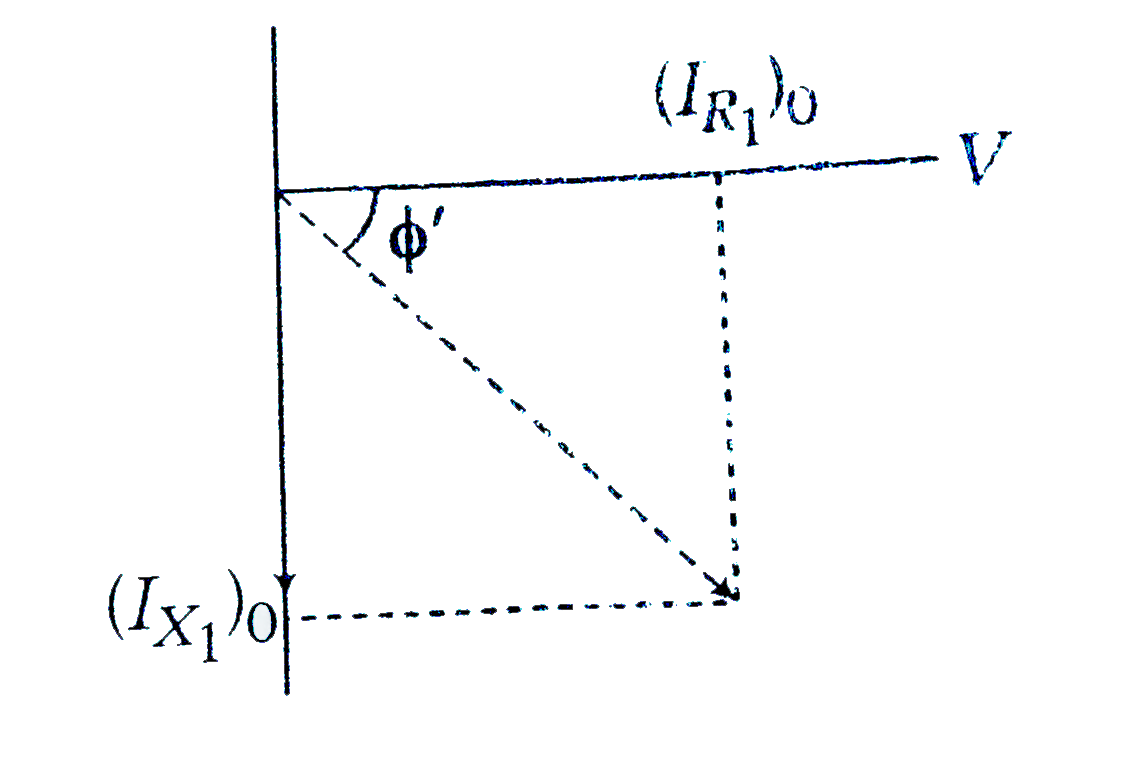
I0=⎛⎝√(IR1)2+(IX1)20=√(V0R1)2+(V0X1)2
⇒V0Z=V0√1R21+1X21⇒Z=1√1R21+1X21=5
tanϕ′=(IXL)0(IR1)0=V0/X1V0/R1=R1X1=tanϕ=43
Putting X1=34R1 in Eq. (i)
⇒1R2+1(34R1)2=152
⇒1R21(1+169)=125=1R2=9(25)2
⇒R1=253Ω
⇒X1=34R1=254Ω
|
Similar Questions
Knowledge Check
In the circuit shown in figure, power developed across 1Ω,2Ω and 3Ω resistance are in the ratio of
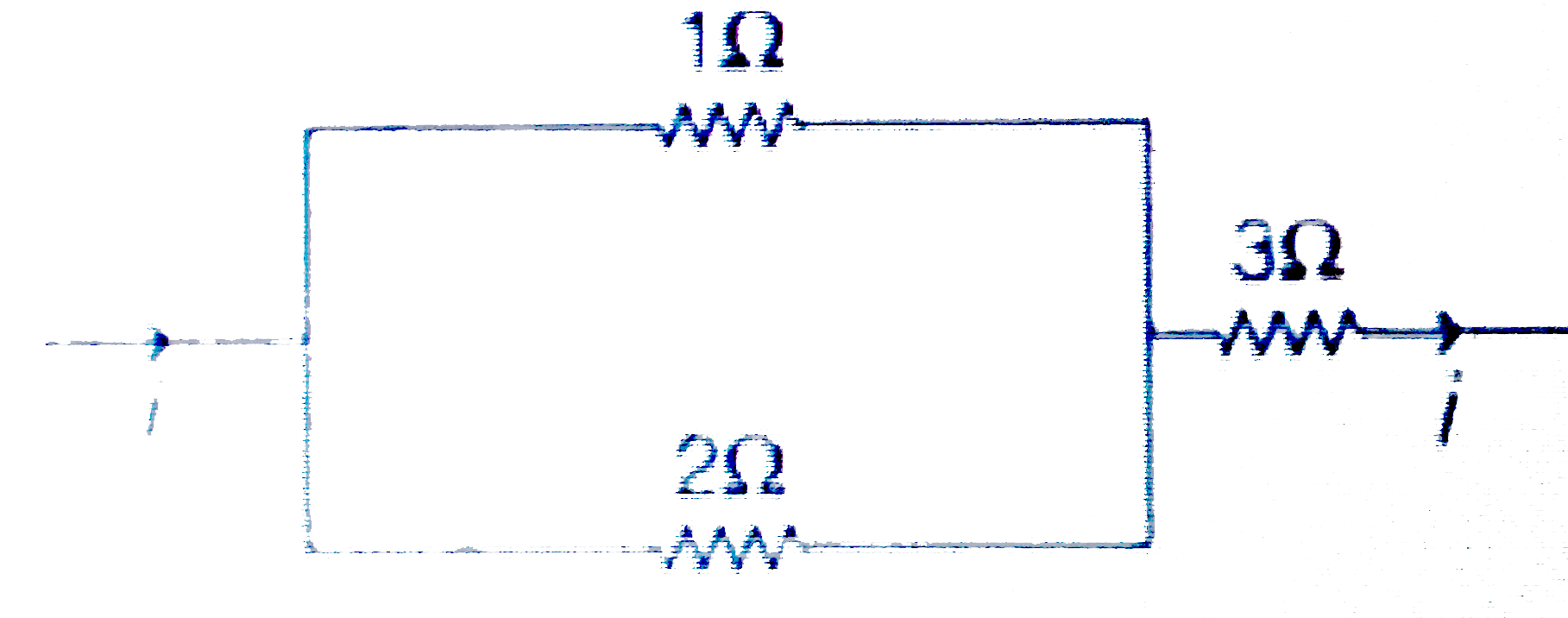 A1:2:3B4:2:27C6:4:9D2:1:27
A1:2:3B4:2:27C6:4:9D2:1:27The impedance of a circuit consister of 3Ωresistance and 4Ω reactance. The power factor of the circuit is
A0.4B0.6C0.8D1The impedance of a series circuit consists of 3ohm resistance and 4ohm reactance.The power factor of the circuit is
A0.4B0.6C0.8D1.0
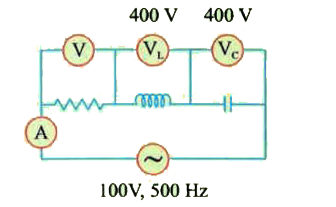
Find the power factor of the circuit shown in figure.
View SolutionIn the circuit,as shown in the figure,if the value of R M S current is 2.2 ampere,the power factor of the box is
View SolutionThe power dissipated in the circuit shown in the figure is 30 W. The value of R is -
View SolutionThere are two circuits shown in figure . Find the ratio of power factor of circuit -I to that with power factor of circuit -II .

View SolutionIn a series LCR circuit, the total reactance is 4Ω and resistance is 3Ω . Its power factor is
View Solution

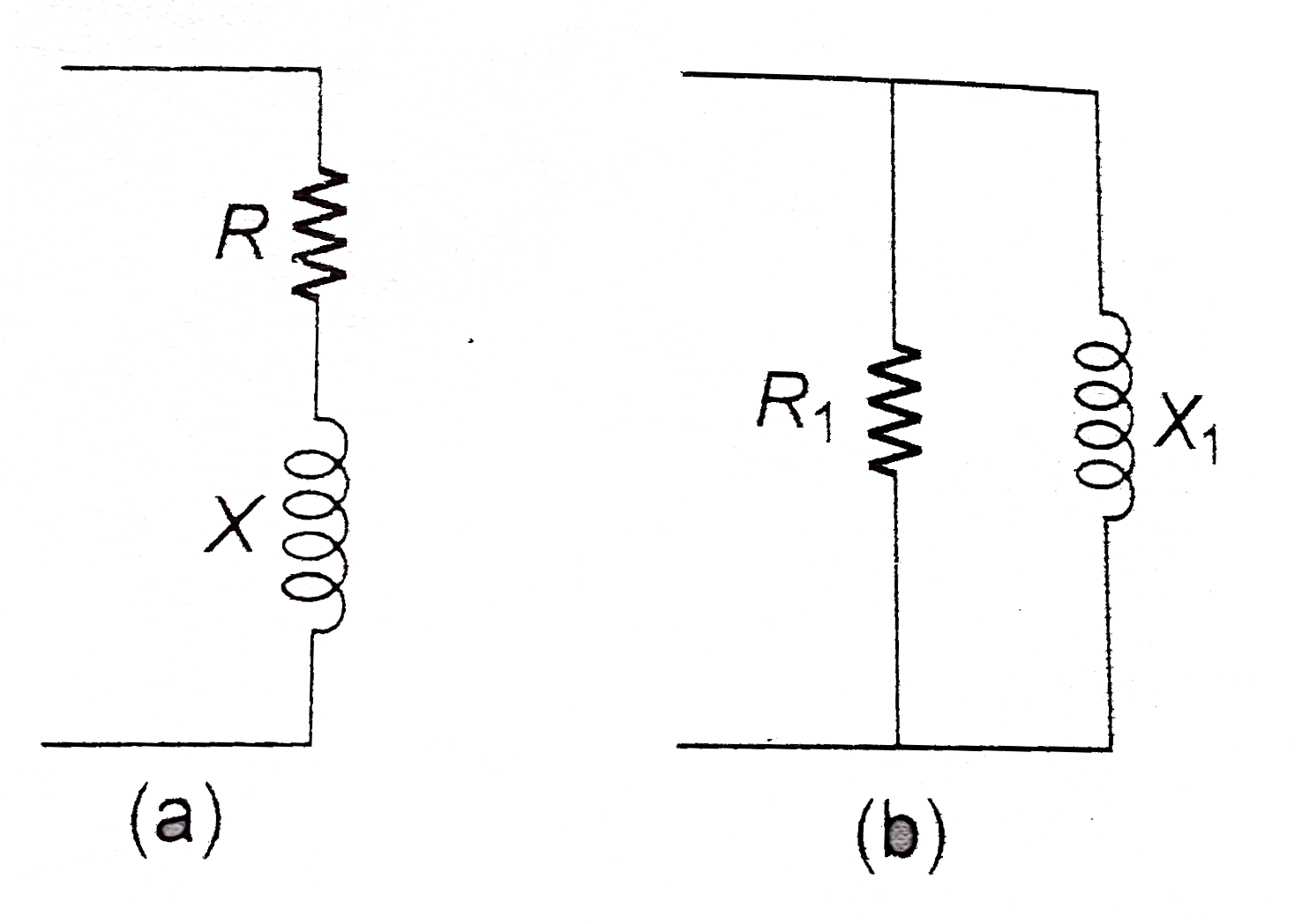 .
.