A conducting rod of length l is moving in a transverse magnetic field of strength B with veocity v. The resistance of the rod is R. The current in the rod is
BlvR
Blv
zero
B2v2l2R
The correct Answer is:C
To find the current in a conducting rod of length l moving in a transverse magnetic field of strength B with velocity v, we can follow these steps:
Step 1: Understand the Concept of Electromagnetic Induction
When a conducting rod moves through a magnetic field, an electromotive force (EMF) is induced in the rod due to electromagnetic induction. This is described by Faraday's law of electromagnetic induction.
Step 2: Calculate the Induced EMF
The induced EMF (E) in the rod can be calculated using the formula:
E=B⋅l⋅v
where:
- B is the magnetic field strength,
- l is the length of the rod,
- v is the velocity of the rod.
Step 3: Relate EMF to Current
The current (I) induced in the rod can be calculated using Ohm's law, which states:
I=ER
where R is the resistance of the rod.
Step 4: Substitute the Induced EMF into the Current Formula
Substituting the expression for EMF into the current formula gives:
I=B⋅l⋅vR
Conclusion
Thus, the current in the rod is:
I=B⋅l⋅vR
Final Answer
The current in the rod is B⋅l⋅vR.
When a conducting rod moves through a magnetic field, an electromotive force (EMF) is induced in the rod due to electromagnetic induction. This is described by Faraday's law of electromagnetic induction.
The induced EMF (E) in the rod can be calculated using the formula:
E=B⋅l⋅v
where:
- B is the magnetic field strength,
- l is the length of the rod,
- v is the velocity of the rod.
The current (I) induced in the rod can be calculated using Ohm's law, which states:
I=ER
where R is the resistance of the rod.
Substituting the expression for EMF into the current formula gives:
I=B⋅l⋅vR
Thus, the current in the rod is:
I=B⋅l⋅vR
The current in the rod is B⋅l⋅vR.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEYChapter:ELECTROMAGNETIC INDUCTIONExercise:Taking it together
Explore 119 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEYChapter:ELECTROMAGNETIC INDUCTIONExercise:Medical entrance special format questions
Explore 17 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEYChapter:ELECTROMAGNETIC INDUCTIONExercise:Level 2 Subjective
Explore 20 Videos
- CURRENT ELECTRICITYBook:DC PANDEYChapter:CURRENT ELECTRICITYExercise:Medical entrances gallery
Explore 97 Videos
- ELECTROMAGNETIC WAVESBook:DC PANDEYChapter:ELECTROMAGNETIC WAVESExercise:Sec C
Explore 22 Videos
Similar Questions
A metal rod of length l cuts across a uniform magnetic field B with a velocity v. If the resistance of the circuit of which the rod forms a part is r, then the force required to move the rod is
View SolutionA rod of length l is moving velocity v "in magnetic field" b as seen in . Find the emf induced in all three cases.
(a)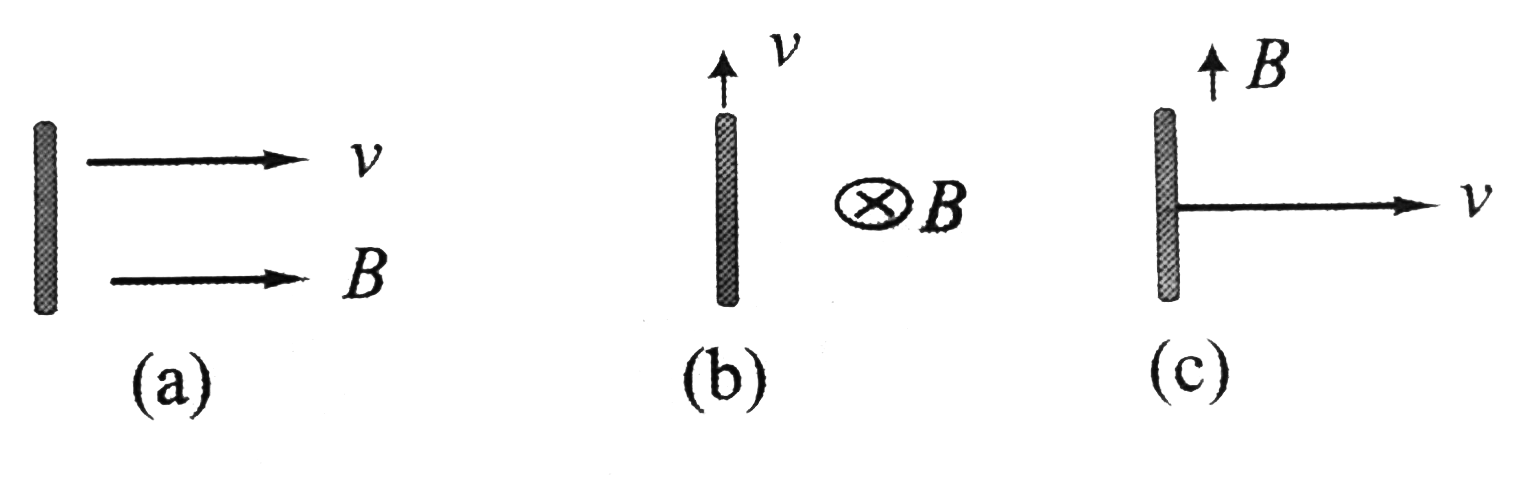
View Solution
Knowledge Check
A uniform rod of mas m is moving with constant velocity v0 in a perpendicular uniform magnetic field B as shown. The resistance of rod is r . The current flowing through rod, RI and R2 will be
 ABv0L3r,23.Bv0L3r,13.Bv0L3rBBv0L3r,13.Bv0L3r,23.Bv0L3rCBv0L3r,13.Bv0L3r,13.Bv0L3rDBv0L3r,Bv0L3r,Bv0L3r
ABv0L3r,23.Bv0L3r,13.Bv0L3rBBv0L3r,13.Bv0L3r,23.Bv0L3rCBv0L3r,13.Bv0L3r,13.Bv0L3rDBv0L3r,Bv0L3r,Bv0L3rA conducting rod of length l and mass m is moving down a smooth inclined plane of inclination θ with constant i is flowing in the conductor in a direction perpendicular to paper inwards. A vertically upward magnetic field →B exists in space. Then, magnitude of magnetic field →B is
 AmgsinθIlBmgtanθIlCmgcosθIlDmgsinθI
AmgsinθIlBmgtanθIlCmgcosθIlDmgsinθIA conducting rod of length 1 is moving on a horizontal smooth surface. Magnetic field in the region is vertically downward and magnitude B0. If centre of mass (COM) of the rod is translating with velocity v0 and rod rotates about COM with angular velocity v0/l, then potential difference between points O and A will be
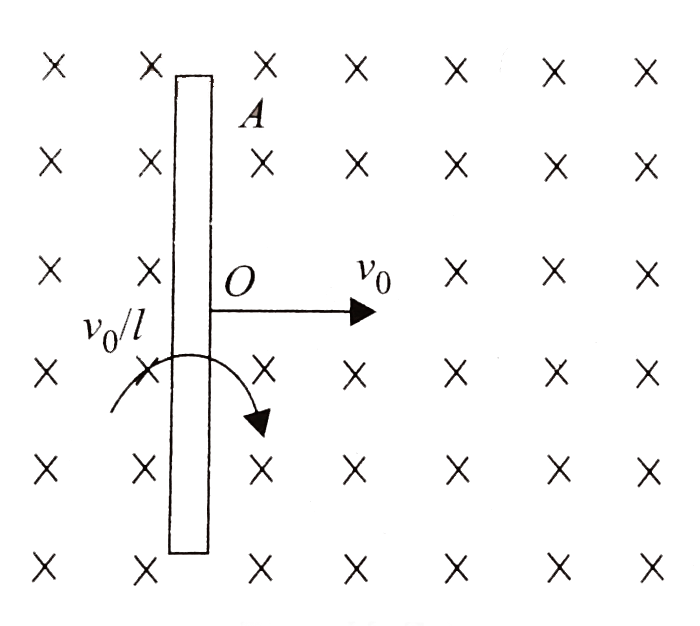 A58B0v0lB38B0v0lC18B0v0lD12B0v0l
A58B0v0lB38B0v0lC18B0v0lD12B0v0l
A conducting circular loop of radius a and resistance per unit length R is moving with a constant velocity v0 , parallel to an infinite conducting wire carrying current i0. A conducting rod of length 2a is approaching the centre of the loop with a constant velocity v02 along the direction 2 of the current. At the instant t=0, the rod comes in contact with the loop at A and starts sliding on the loop with the constant velocity. Neglecting the resistance of the rod and the self-inductance of the circuit, find the following when the rod slides on the loop.

(a) The current through the rod when it is at a distance of (a2) from the point A of the loop.
(b) Force required to maintain the velocity of the rod at that instant.
View SolutionA conducting rod of length l is moving perpendicular to magnetic field.The rod moves from 0 to 2b while field exists only from 0 to b. Find the graph for emf and power dissipated w.r.t x.
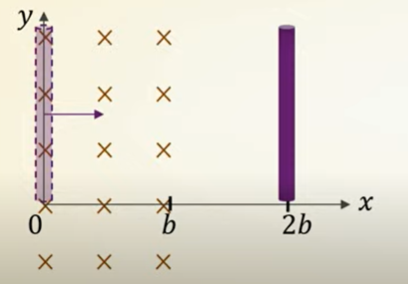
View Solutiona conducting rod of length L=30.0cm movies in a magnetic field →B of magnitude 0.450T directed into the plane of the figure. The rod moves with speed v=5.00ms−1 in the direction shown.
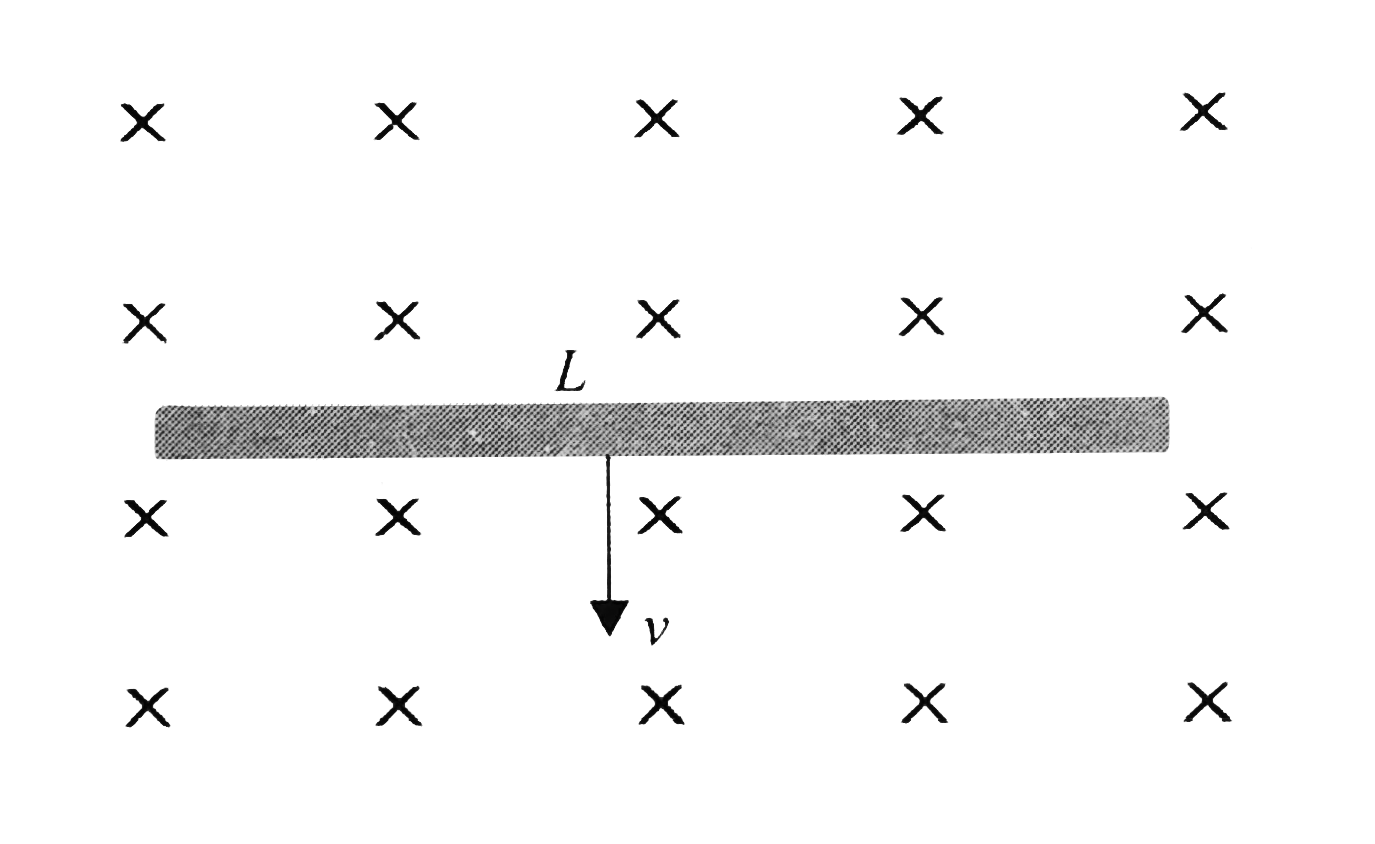
(a) What is motional emf inuced in the rod ?
(b) What is the potential difference between the ends of the rod?
( c) When point, aorb, is at higher potential?
(d) When the charges in the rod are in equilibrium, what are the magnitude and direction of the electric field within the rod?
(e) When the charges in the rod are in the rod in equilibrium, which point, aorb, has an excess of positive charge?
View SolutionA glass rod of length l moves with velocity in a uniform magnetic field B. What is the e.m.f. induced in the rod ?
View SolutionA conducting rod of length L is carrying a constant current I. There exists a magnetic field B perpendicular to the rod. Due to the magnetic force the rod moved through a distance x in a direction perpendicular to the field (B) as well as its own length. The rod acquires a kinetic energy. A student says that a magnetic force ILB acted on the rod and it performed a work W=ILBx on the rod. But we know that magnetic force is always perpendicu- lar to the velocity of the charge and it cannot perform work on a moving charge. Which agency has actually spent energy to impart kinetic energy to the rod?
View Solution

