The plane of dip circle is set in the geographic meridian and the apparent dip is θ1. It is then set in a vertical plane perpendicular to the geographic meridian. Now, the apparent dip is θ2. The angle of declination θ at that place is
A
θ=tan−1(tanδ1tanδ2)
B
θ=tan−1(tanδ1+tanδ2)
C
θ=tan−1(tanδ1tanδ2)
D
θ=tan−1(tanδ1−tanδ2)
Video Solution
Text Solution
The correct Answer is:C
Here,tanδ1=VHcosθ
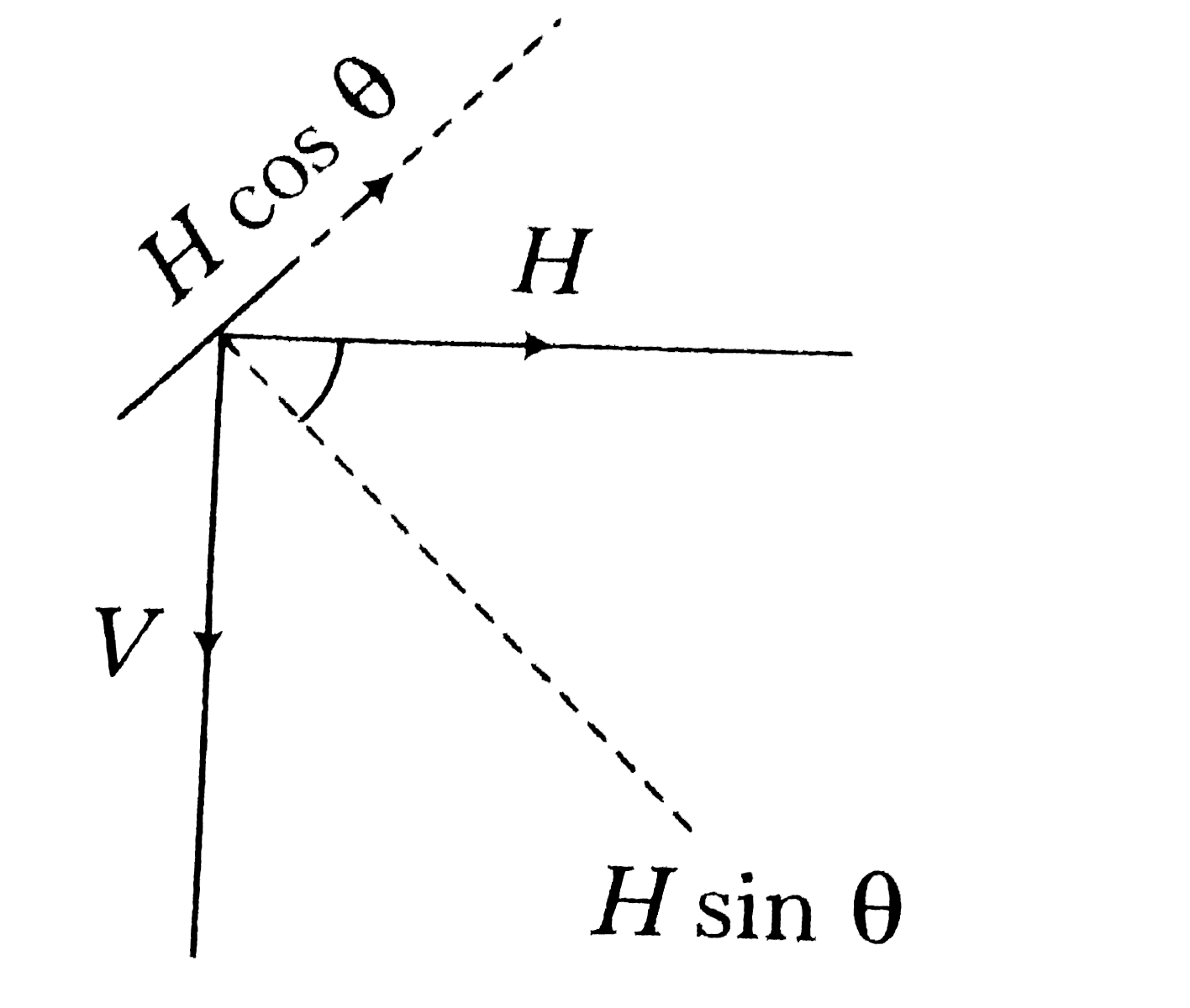
tanδ2=VHcos(90∘−θ)=VHsinθ
tanδ2tanδ2=sinθsinθ=tanθ
θ=tan−1(tanδ1tanδ2)
|
Updated on:21/07/2023
Similar Questions
Knowledge Check
- Question 1 - Select One
In a plane perpendicular to the magnetic meridian, the dip needle will be:
AverticleBinclined equal to the angle of dip at that placeChorizontalDpointing in any direction - Question 2 - Select One
A dip needle free to move in a vertical plane perpendiculr to the magneetic meridian will remain
AHorizontalBVerticalCAt an angle of 60∘ to the verticalDAt an angle of 45∘ to the horizontal - Question 3 - Select One
A dip needle in a plane perpendicular to magnetic meridian will remain
AVerticalBHorizontalCIn any directionDAt an angle of dip to the horizontal
At 45∘ to the magnetic meridian the apparent dip is 60∘. The true dip is
View SolutionA dip needle in a plane perpendicular to magnetic meridian will remain
View SolutionA dip circle is at right angles to the magnetic meridian. What will be the apparent dip ?
View SolutionA dip cicrle is at right angles to the magnetic meridian. What will be the apparent dip ?
View SolutionA dip circle is taken to geomagnetic equator. The needle is allowed to move in a vertical plane perpendicular to the magnetic meridian. The needle will stay
View Solution

