A spherical ball of radius 3×10−4m and density 104kg/m3 falls freely under gravity through a distance h before entering a tank of water. If after entering the water the velocity of the ball does not change, find h the viscosity of water is 9.8×10−6N−s/m2
1.65×103m
2.65×102m
3.65×104m
1.45×102m
The correct Answer is:A
Before entering the water the velocity of ball is √2gh. If after entering the water this velocity does not change, then this value should be equal to the terminal velocity. Therefore,
√2gh=29r2(ρ−σ)gη
∴h={29r2(ρ−σ)gη}22g=281×r4(ρ−σ)2gη2
=281×(3×10−4)4(104−103)2×9.8(9.8×10−6)2=1.65×103m
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Check point 13.4
10 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Taking it together
157 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Check point 13.2
10 Videos
- EXPERIMENTSBOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A spherical ball of radius 3.0×10−4m and density 104kg/m3 falls freely under gravity through a distance h before entering a tank of water. If after entering the water the velocity of the ball does not change, find h. Viscosity of water is 9.8×106N−s/m2.
View SolutionA spherical ball of radius 3.0×10−4 m and density 104kgm3 falls freely under gravity through a distance H=n×500m before entering a tank of water. If after enerting the water the velocity of the ball does not change, then find n. viscosity of water is 10×10−6N−sm2,g=10ms
View Solution
Knowledge Check
A metal ball ofradius 10−4 m and density 104kg/m3 falls freely under gravity through a distance 'h' and enters a tank of water. It is found that after entering the water, the velocity of ball does not change. What is the value of h?
[ηfor water 10−5 Pas ,g=10m/s2 and orhwater=103kg/m3]A10mB15mC18mD20mA drop of radius 2×10−5 and density 1.2×103kg/m3 falls through air. The viscosity of air is 1.8×10−5Ns/m2. Neglecting buoyancy due to air, the terminal speed of the drop is
A2.8cm/sB3.8cm/sC4.8cm/sD5.8cm/sA sphere of radius 10cm and density 500kg/m3 is under water of density 1000kg/m3 The acceleration of the sphere is 9.80m/s2 upward viscosity of water is 1.0 centipoise if g=9.81m/s2 the velocity of the sphere is
A9m/sB10m/sC11m/sD12m/s
A small ball of radius 'r' falls freely under gravity through a distance 'h' before entering a tank of water. If after entering the water, the velocity of ball does not change, the 'h' is proportional to
View SolutionA small ball of radius 'r' falls freely under gravity through a distance 'h' before entering a tank of water. If after entering the water, the velocity of ball does not change, the 'h' is proportional to
View SolutionA ball of radius r and density r falls freely under gravity through a distance h before entering water. Velocity of ball does not change even on entering water. If viscosity of water is η the value of h is given by
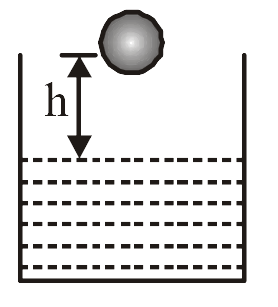
View SolutionIn an experiment to verify Stokes law , a small spherical ball of radius r and density ρ falls under gracvity throught a distance h in air before entering a tank of wate . If the terminal velocity of the ball inside water is same as its velocity just befor entering the water surface , then the value of h is proportional to : ( ignore viscosity of air ) .
View SolutionA metallic sphere of radius 1.0×10−3m and density 1.0×104kg/m3 enters a tank of water, after a free fall through a distance of h in the earth's gravitational field. If its velocity remains unchanged after entering water, determine the value of h. Given: coefficient of viscosity of water =1.0×10−3Ns/m2,g=10ms−12 and density of water =1.0×103kg/m3.
View Solution
