A recantangular frame is to be suspended symmetrically by two strings of equal length on two supports (figure).It can be done in one of the following three ways:
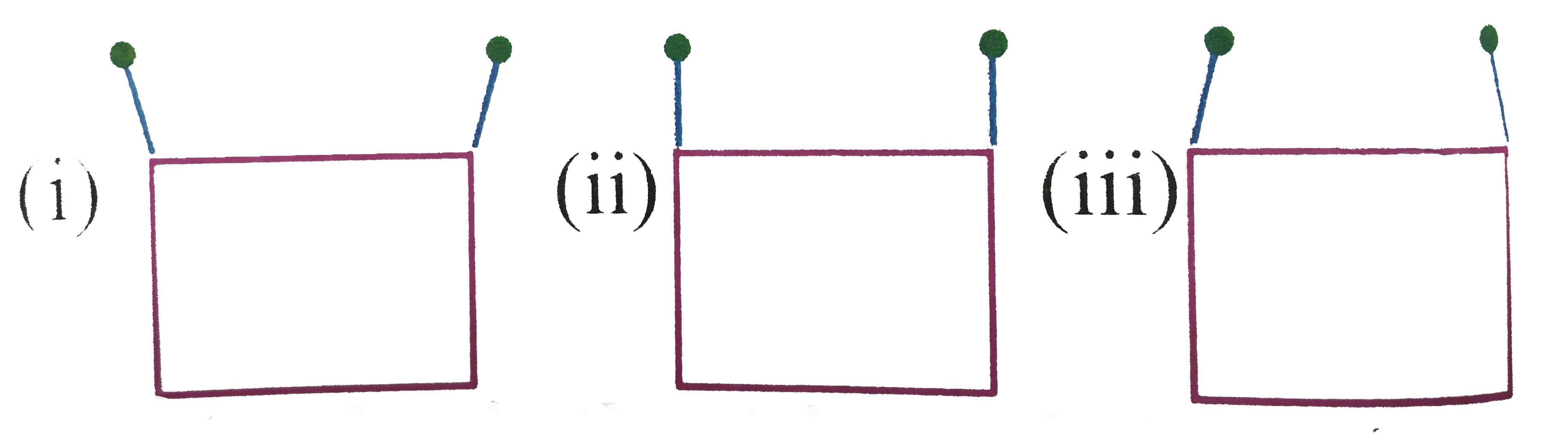
the same in all cases
least in (a)
least in (b)
least in (c)
The correct Answer is:C
(c) Consider the FBD diagram of the rectangular frame
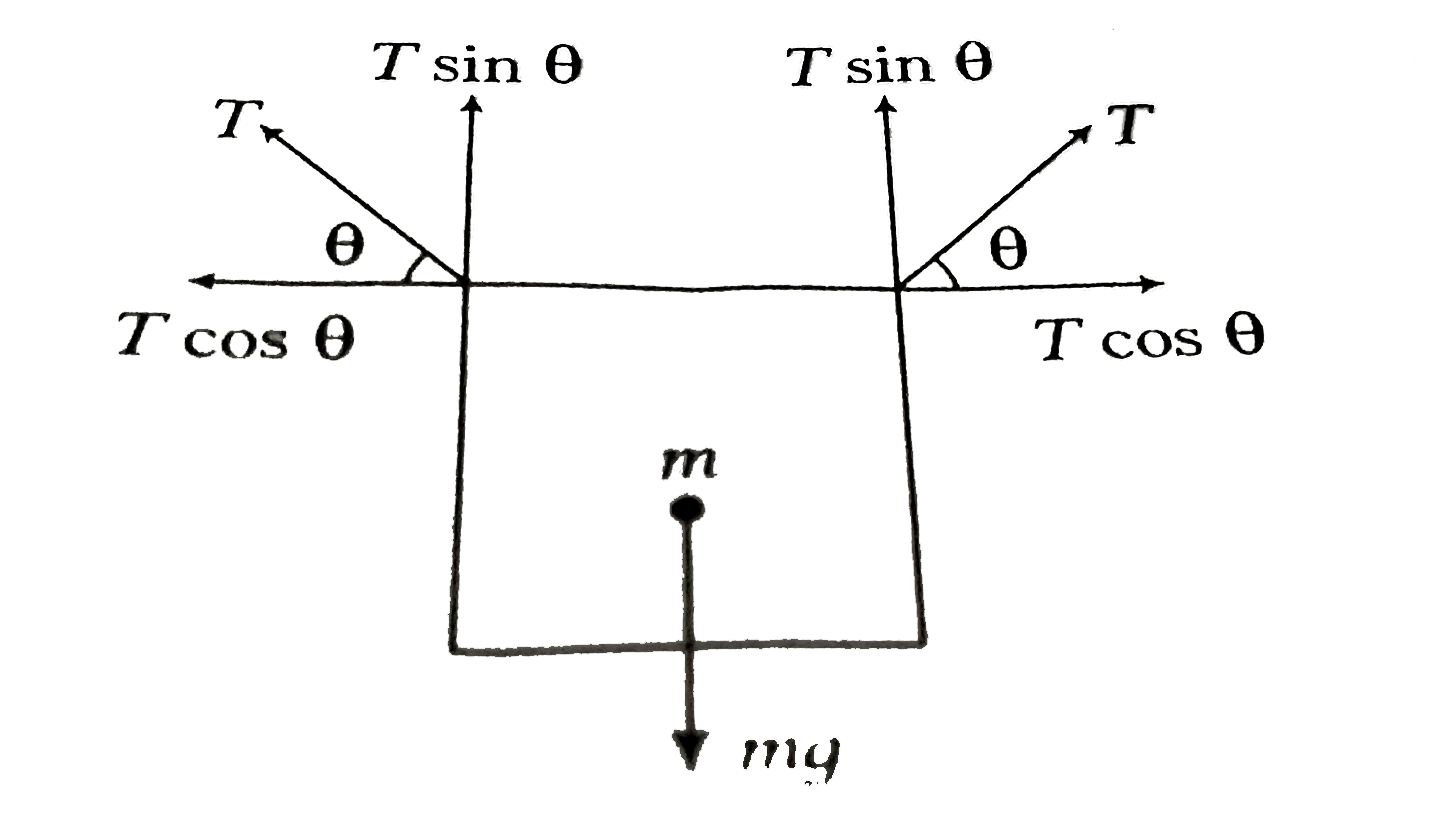
Balancing vertical force 2Tsinθ−mg=0 [T is tension in the string]
⇒ 2Tsinθ=mg
Total horizontal force =Tcos θ−Tcos θ=0
Now from Eq. (i) T=mg2sinθ
As mg is constant
⇒T∝1sinθ
⇒sinθmin=0⇒θmax=0
No option matches with θ=0∘
Tmin=mg2sinθmax (since sinθmax=1)
sinθmax=1⇒θ=90∘
Matches with option (b).
Hence , tension is least for the case (b).
Note We should be careful when measuring the angle, it must be in the direction as given in the diagram.
Topper's Solved these Questions
- ELASTICITYBOOK - DC PANDEYCHAPTER - ELASTICITYEXERCISE - Match the columns
4 Videos
- ELASTICITYBOOK - DC PANDEYCHAPTER - ELASTICITYEXERCISE - Medical entrances s gallery
21 Videos
- ELASTICITYBOOK - DC PANDEYCHAPTER - ELASTICITYEXERCISE - Check point 12.3
15 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
434 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
Similar Questions
Two indentical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
View SolutionTwo identical balls having equal positive charge q coulomb are suspended by two in painting strings of equal length. What would be the effect on the force when a plastic sheet is inserted between the two?
View Solution
Knowledge Check

A rod is supported horizontally by means of two strings of equal length as shown in figure. If one of the string is cut. Then tension in other string at the same instant will.Aremains unaffectedBincreaseCdecreaseDbecome equal to weight of the rod.A uniform rod of length 3L and mass m is suspended from a horizontal roof by two strings of length L and 2L as shown. Then the tension in the left string of length L is :
 AmgBmg4Cmg2Dmg3
AmgBmg4Cmg2Dmg3Two spherical objects each of radii R and masses m1 and m2 are suspended using two strings of equal length L as shown in the figure (R<<L). The angle, θ which mass m2 makes with the vertical is approximately -
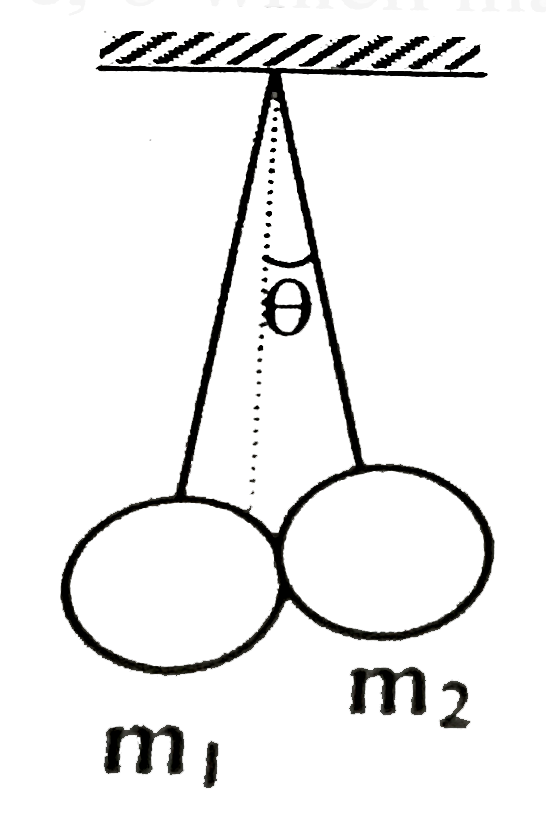 Am1R(m1+m2)LB2m1R(m1+m2)LC2m2R(m1+m2)LDm2R(m1+m2)L
Am1R(m1+m2)LB2m1R(m1+m2)LC2m2R(m1+m2)LDm2R(m1+m2)L
Two small balls having equal poistive charges Q( coulomb) on each are suspended by two insulating strings of equal length L(metre) from a hook fixed to a stand. The whole set up is taken in a satellite into space where there is no gravity (state of weightlessness). The angle between the two strings is...............and the tenison in each string is...................newtons.
View SolutionA rigid bar of mass M is supported symmetrically by three wires each of length l. Those at each end are of copper and the middle one is of iron. The ratio of their diameters, if each is to have the same tension, is equal to
View SolutionA rigid bar of mass M is supported symmetrically by three wires each of length l. Those at each end are of copper and the middle one is of ion. The ratio of their diameters, if each is to have the same tension, is equal to
View SolutionA rigid bar of mass M is supported symmetrically by three wires each of length l. Those at each end are of copper and the middle one is of iron. The ratio of their diameters, if each is to have the same tension, is equal to
View SolutionTwo equal masses are attached to the two ends of a spring of spring constant k. The masses are pulled out symmetrically to stretch the spring by a length x over its natural length. The work done by the spring on each mass is
View Solution
