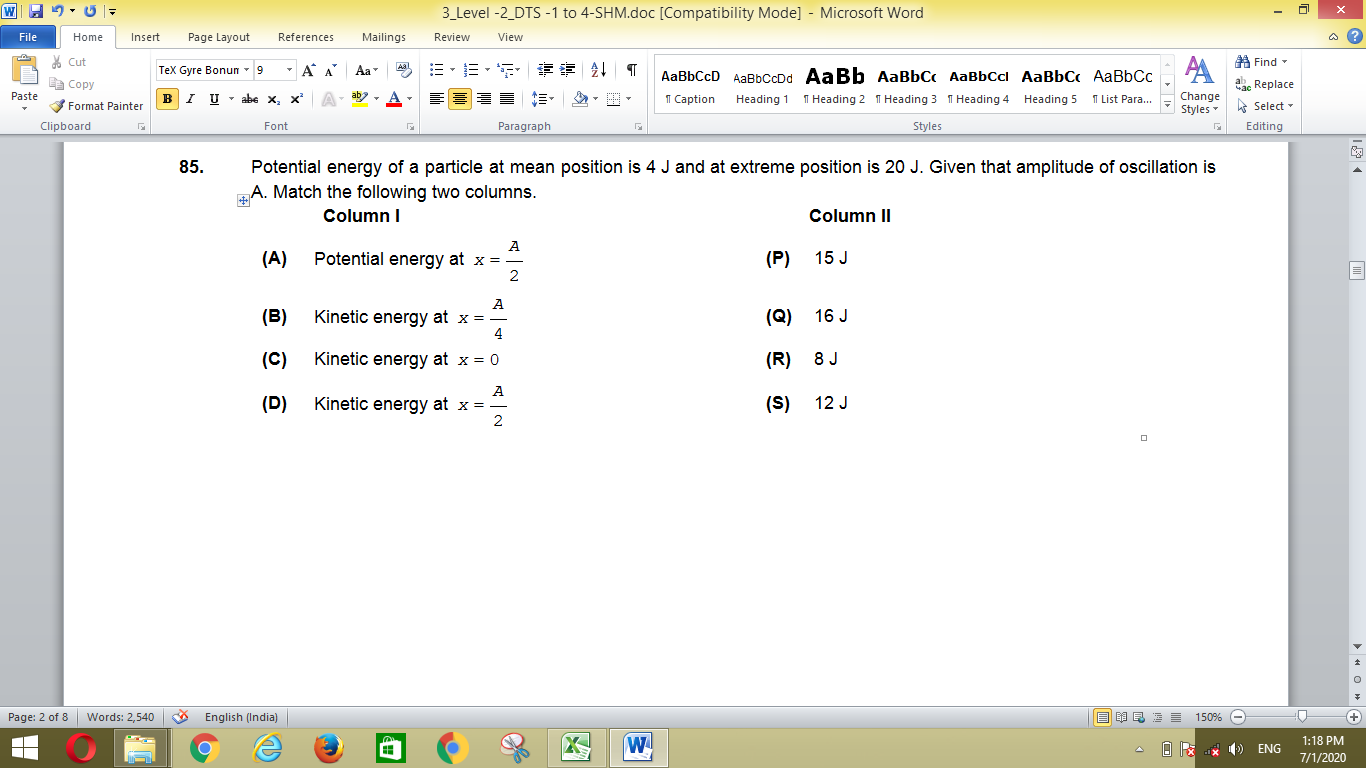
x-t equation of a particle in SHM is given as x= $1.0 sin (12 π t)$ in SI units. Potential energy at mean position is zero. Mass of particle is $\frac{1}{4}$ kg. Match the following table (SI units).

Video Solution

Text Solution

Verified by Experts

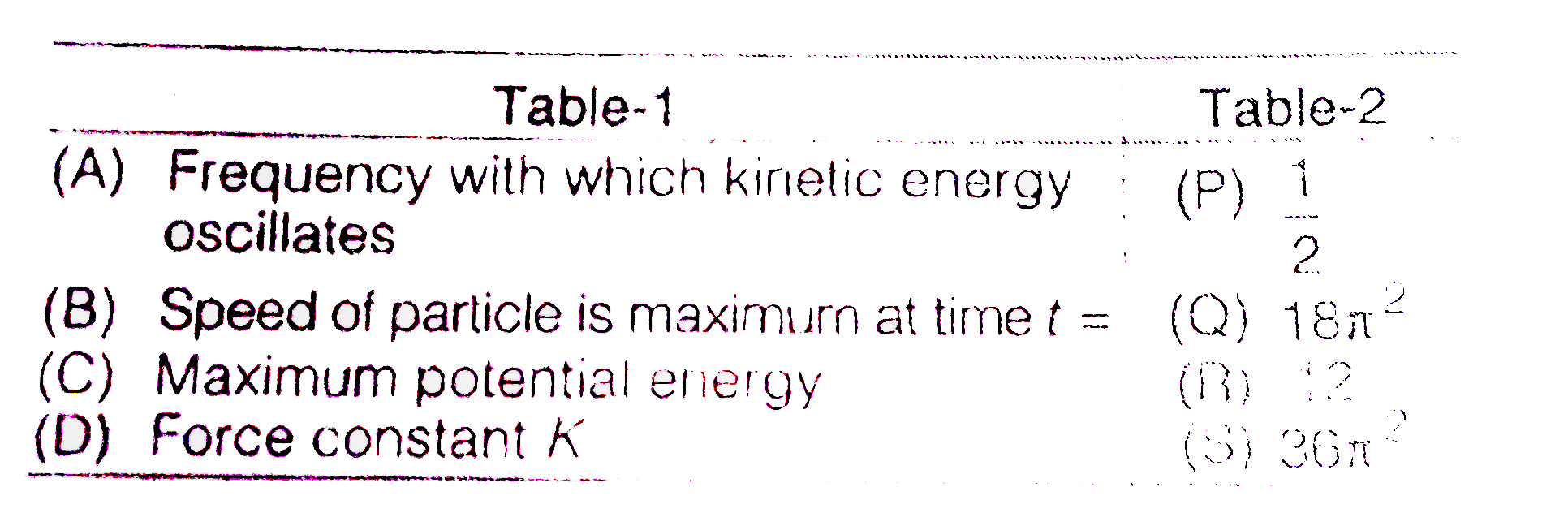
The correct Answer is: $(A \to r, B \to p, C \to q, D \to s)$

Updated on:21/07/2023

Answer

Step by step video, text & image solution for x-t equation of a particle in SHM is given as x=1.0sin(12pit) in SI units. Potential energy at mean position is zero. Mass of particle is 1/4 kg. Match the following table (SI units). by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Knowledge Check

Assertion : x-t equation of a particle in SHM is given as : $x = A cos ω t$
Reason : In the given equation the minimum potential energy is zero.
AIf both Assertion and Reason are correct and Reason is the correct explanation of Assertion.
BIf both Assertion and Reason are correct but Reason is not the correct explanation of Assertion.
CIf Assertion is true but Reason is false.
DIf Assertion is false but Reason is true.
In SHM , potential energy of a particle at mean position is $E_{1}$ and kinetic enregy is $E_{2}$ , then
A $E_{1} = E_{2}$
Btotal potential energy at $x = \frac{\sqrt{3} A}{2}$ is $E_{1} + \frac{3 E_{2}}{4}$
Ctotal kinetic energy at $x = \frac{\sqrt{3} A}{2}$ is $\frac{3 E_{2}}{4}$
Dtotal kinetic energy at $x = \frac{A}{\sqrt{2}}$ is $\frac{E_{2}}{4}$
A particle of mass 1 kg executing S.H.M. is given by y = 2 cos $(10 t + π / 3)$ in SI units. Its maximum potential energy is
A2 J
B20 J
C200 J
D100 J

x-t equation of a particle in SHM is given as x= $1.0 sin (12 π t)$ in SI units. Potential energy at mean position is zero. Mass of particle is $\frac{1}{4}$ kg. Match the following table (SI units).

The correct Answer is: $(A \to r, B \to p, C \to q, D \to s)$

Similar Questions

Knowledge Check

Assertion : x-t equation of a particle in SHM is given as : $x = A cos ω t$
Reason : In the given equation the minimum potential energy is zero.

In SHM , potential energy of a particle at mean position is $E_{1}$ and kinetic enregy is $E_{2}$ , then

A particle of mass 1 kg executing S.H.M. is given by y = 2 cos $(10 t + π / 3)$ in SI units. Its maximum potential energy is

Recommended Questions

x-t equation of a particle in SHM is given as x=1.0sin(12πt) in SI units. Potential energy at mean position is zero. Mass of particle is 14 kg. Match the following table (SI units).

The correct Answer is:(A→r,B→p,C→q,D→s)

Similar Questions

Knowledge Check

Assertion : x-t equation of a particle in SHM is given as :x=Acosωt Reason : In the given equation the minimum potential energy is zero.

In SHM , potential energy of a particle at mean position is E1 and kinetic enregy is E2 , then

A particle of mass 1 kg executing S.H.M. is given by y = 2 cos (10t+π/3) in SI units. Its maximum potential energy is

Recommended Questions

x-t equation of a particle in SHM is given as x= $1.0 sin (12 π t)$ in SI units. Potential energy at mean position is zero. Mass of particle is $\frac{1}{4}$ kg. Match the following table (SI units).

The correct Answer is: $(A \to r, B \to p, C \to q, D \to s)$

Assertion : x-t equation of a particle in SHM is given as : $x = A cos ω t$
Reason : In the given equation the minimum potential energy is zero.

In SHM , potential energy of a particle at mean position is $E_{1}$ and kinetic enregy is $E_{2}$ , then

A particle of mass 1 kg executing S.H.M. is given by y = 2 cos $(10 t + π / 3)$ in SI units. Its maximum potential energy is