STATEMENT-1 : In simple harmonic motionn graph between celocity (v) and displacement (x) from mean position is elliptical.
STATEMENT-2 : Relation between v and x is given by v2ω2A2+X2A2=1.
If both Assertion and Reason are correct and Reason is the correct explanation of Assertion.
If both Assertion and Reason are correct but Reason is not the correct explanation of Assertion.
If Assertion is true but Reason is false.
If Assertion is false but Reason is true.
The correct Answer is:A
(a) v=a√A2−x2
∴v2ω2+x21=A2
Similar Questions
The velocity-displacement graph of a particle is shown in the figure. Write the relation/equation between v and x.
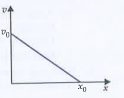 .
.
View SolutionThe figure shows graph between velocity 'V' and displacement 'X' from mean position of a particle performing simple harmonic motion

The time period of motion of particle is:
View Solution
Knowledge Check
STATEMENT-1 : In simple harmonic motion, at extreme position the velocity and acceleration of object is zero.
STATEMENT-2 : In simple harmonic motion at mean position?AStatement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1.BStatement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-1.CStatement-1 is True, Statement-2 is False.DStatement-1 is False, Statement-2 is True.If a graph is plotted between velocity (v) and displacement (y) of a particle executing SHM from mean position, then the nature of the graph is
AStraight lineBParabolaCEllipseDHyperbolaStatement-I : In simple harmonic motion, the graph between velocity and the displacement is an ellipse.
Statement-II : In simple harmonic motion the phase difference between velocity and displacement is π/2.AStatement-I is true, Statement-Ii is true, Statement-II is a correct explanation for Statement-I.BStatement-I is true, Statement-II is true, Statement-II is NOT a correct explanantion for Statement-I.CStatement-I is true, Statement-II is falseDStatement-I is false, Statement-II is true
STATEMENT-1 : A particle is performing simple harmonic motion along X axis with amplitude A. If a graph is plotted between velocity of particle and its X coordinate then graph will be elliptical.
STATEMENT-2 : Velocity of particle in SHM as a fuction of position is given by
v=ω√A2−X2.
View SolutionA particle is performing harmonic motion if its velocity are v1 and v2 at the displecement from the mean position are y1 and y2 respectively then its time period is
View SolutionThe figure shows graph between velocity 'V' and displacement 'X' from mean position of a particle performing simple harmonic motion

The velocity of particle when it is at a distance 1.5m from mean position is :
View SolutionA body is executing simple harmonic motion. At a displacement x from mean position, its potential energy is E1=2J and at a displacement y from mean position, its potential energy is E2=8J. The potential energy E at a displacement (x+y) from mean position is
View SolutionA simple harmonic oscillator has amplitude 2 A and maximum velocity 2 V. Then its displacement at which its velocity is V and the velocity at displacement A are
View Solution