Two cyllindrical vessels of equal cross sectional ara A contain water upto heights h1 and h2. The vessels are interconnected so that the levels in them become equal. Calculate the work done by the force of gravity during the process. The density of water is ρ
According to the question, we draw the following diagram. 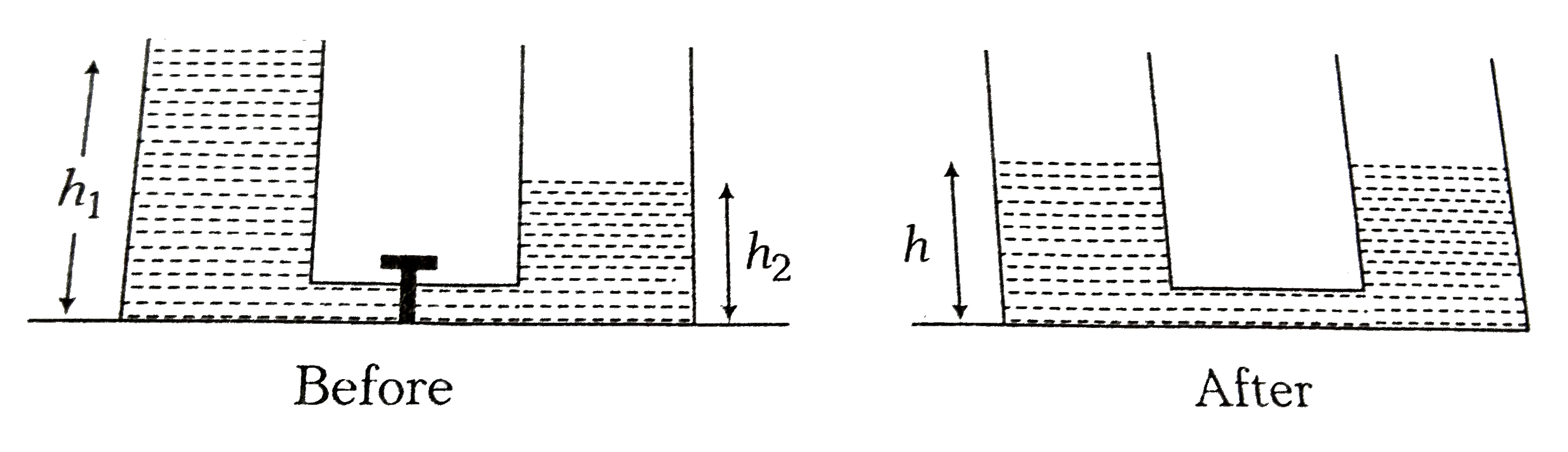
Since the mass of water remains same
ρAh1+ρAh2=ρAh+ρAh⇒h=h1+h22
Potential energy of first vessel
U1=(ρAh1)gh12+(ρAh2)gh22=ρAg2(h21+h22) Potential energy of second vessel
U2=(ρAh)gh2×2=ρAg(h1+h2)24
Since the gravitational force is a conservative force, then
Wgr=U1−U2=ρAg4(h1−h2)2
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - CHECK POINT 6.1
20 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - CHECK POINT 6.2
20 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEYCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions
11 Videos
Similar Questions
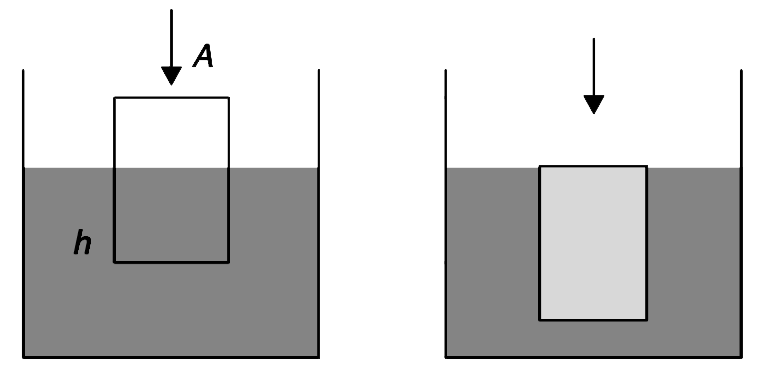
A cylindrical wooden block of density half the density of water is floating in water in a cylindrical container. The cross section of the wooden block. And its height are A and h respectively. The cross sectional area of the container is 2A. The wooden block is pushed vertically so that it gradually gets immersed in water. Calculate the amount of work done in pushing the block. Density of water =ρ0.
View SolutionTwo identical cylindrical vessels with their bases at the same level each, contain a liquid of density ρ. The area of either base is A but in one vessel the liquid heigth is h1 and in the other liquid height is h2(h2<h1). If the two vessel are connected, the work done by gravity in equalizing the level is
View Solution
Knowledge Check
Two cylindrical vessels of equal cross-sectional area. A contain water upto height h1 and h2. The vessels are interconnected so that the levels in them becomes equal. The work done by the force of gravity during the process is:
AzeroBρA(h1+h22)2gCρA(h1−h22)2gDρAh1h22gA cylindrical vessel of cross section A contains water to a height h. There is a hole in the bottom of radius 'a'. The time in which it will be emptied is:
A2Aπa2√hgB√2Aπa2√hgC2√2Aπa2√hgDA√2πa2√hgWater rises upto a height h in a capillary tube of radius r. What is the network done in this process if the density of water is ρ ?
Aπr2h2ρg2Bπr2hρgC2πr2hρgDπr2gρg2
Two vessels of equal volume contain milk and water in the ratio 1:3 and 2:1. If they are mixed together what is the new ratio?
View SolutionA cylindrical vessel of uniform cross-section contains liquid upto the height' H’ . At a depth H=H2 below the free surface of the liquid there is an orifice. Using Bernoulli's theorem, find the velocity of efflux of liquid.
View SolutionMercury of density ρm is poured into cylinderical communicating vessels of cross-sectional area 2A and A respectively. A solid iron cube of volume V0 and relative density 2 is dropped into the broad vessel, and as a result the level of the mercury in it rises. Then, water is poured into the broader vessel until the mercury reaches the previous level in it. Find the height of water column if it does not submerge the block.
View SolutionA liquid of density ρ is filled in two indentical cylindrical vessels with base area A and height of the liquid in one vessel is h1 and that in the other vessel is h2. If both the vesels are connected with their base at the same level then calculate the work done by gravity in equalizing the levels.
View SolutionA capillary tube of area of cross-section A is dipped in water veritcally. Calculate the amount of heat evolved as the water rises in the capillary tunbe upto height h. The density of water is ρ
View Solution
