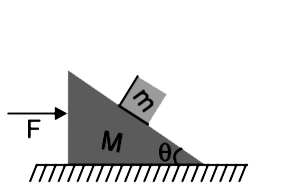
All surfaces are smooth in following figure. Find F, such that block remain stationary with respect to wedge.

F=(M+m)gtanθ
F=(M−m)gtanθ
F=M+mgtanθ
F=(M+m)gsinθ
The correct Answer is:A
Acceleration of (block+ wedge)
a=F(M+m)
Let us solve the problem by both the methods.
(i) From Inertia Frame of Reference (Ground) FBD of block w.r.t. ground (apply real forces) with respect to ground, block is moving with an acceleration a

∴∑Fy=0
⇒Ncosθ=mg...........(i)
and ∑Fx=ma
⇒Nsinθ=ma............(ii)
From Eqs. (i) and (ii)
a=gtanθ
∴F=(M+m)a
=(M+m)gtanθ
(ii) From Non-inertial Frame of Reference (Wedge) FBD of block w.r.t. wedge (real forces + pseudo force)
(##ARHN∃TPHYOBJV01C05S01027_S02.png width=80%><br>w.r.t.∧,blockisstatio≠ry<br>therefore sumF_(y)=0 implies N cos theta=mg............(iii)<br>sum F_(x)=0 implies N sin theta= ma...............(iv)<br>Inthiswaytheblock's≠tae≤rationbecomeszero∵alltheforcesact∈gonthembalanceeachotherforanobserveronthe∧and¬foranobserverontheground.<br>FromEqs.(iii)and(iv),wewill≥tthesamerest–<br>i.e.,F=(M+m)g tan theta.
Topper's Solved these Questions
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Check point 5.1
Explore 20 Videos
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Check point 5.2
Explore 15 Videos
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Subjective Question
Explore 27 Videos
- KINEMATICS 1Book:DC PANDEYChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEYChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
Similar Questions
Knowledge Check
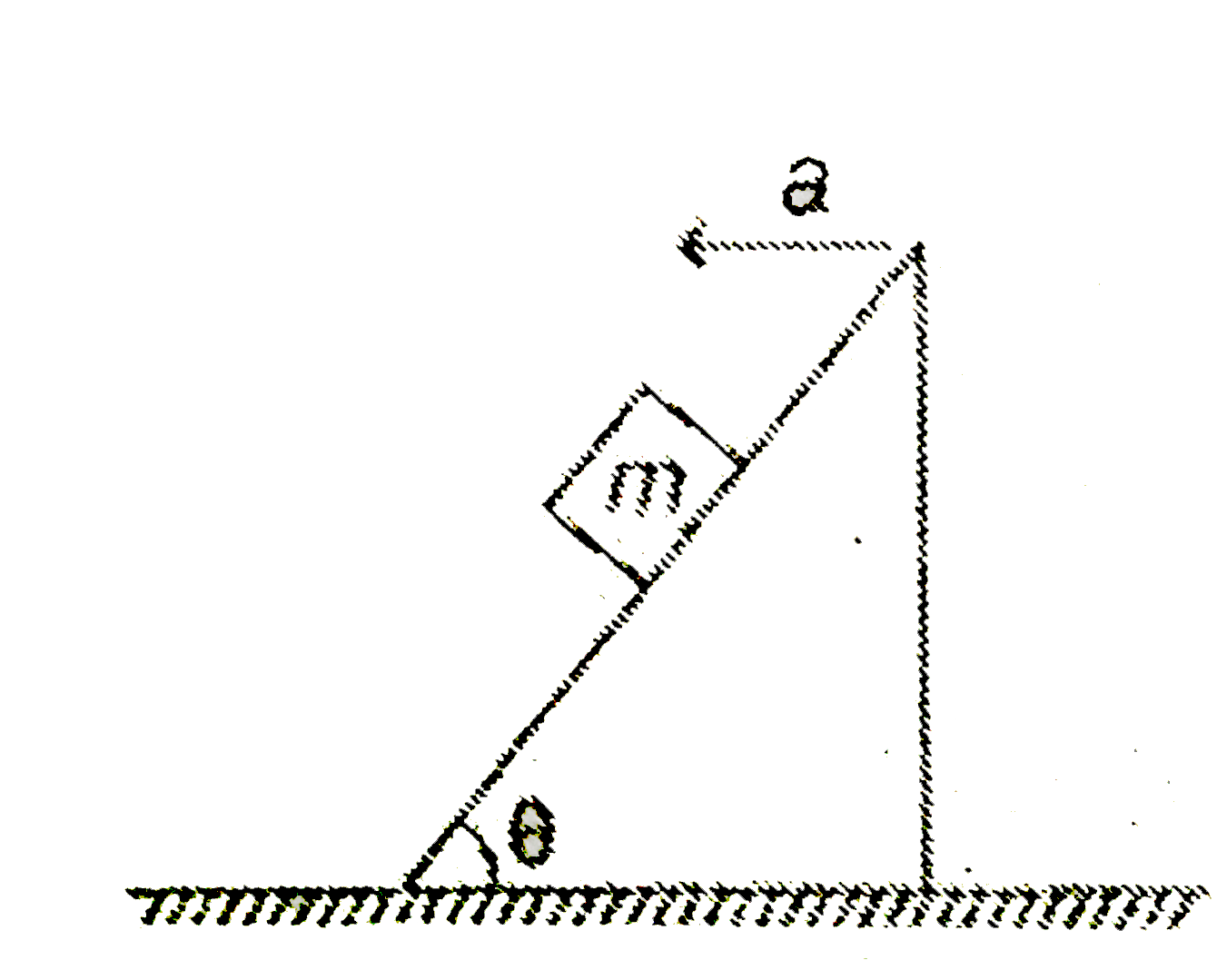
A wooden wedge of mass M and inclination anlgle(α) rest on a smooth floor. A block of mass m is kept on wedge.A force F is applied on the wedge as shown in the figure such that block remains stationary with respect to wedge So, magnitude of froce F is
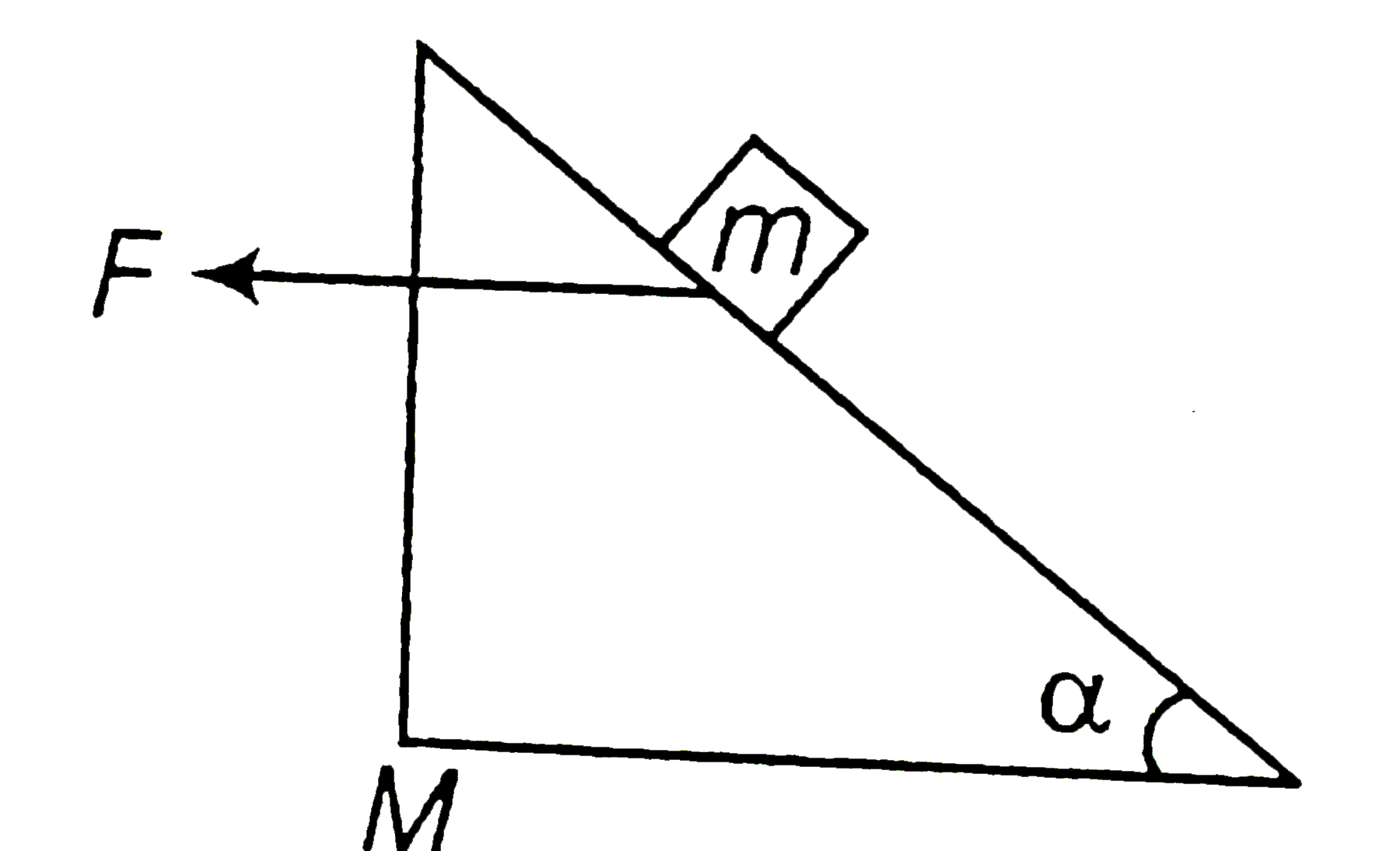 A(M+m)g tan αBg tan αCmg cos αD(M+m)g cosec α
A(M+m)g tan αBg tan αCmg cos αD(M+m)g cosec αIn the given situation, what is the minimum mass of block A so that block B remains stationary with respect to the wall? The coefficient of friction is μ between wall and block. All other surfaces are smooth.
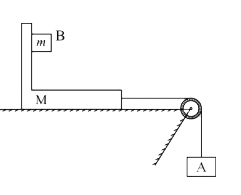 A(M+m)μ+1BMμ−1CM+mμD(M+m)μ−1
A(M+m)μ+1BMμ−1CM+mμD(M+m)μ−1Two wooden blocks are moving on a smooth horizontal surface such that the mass m remains stationary with respect too block of mass M as shown in the figure. The magnitude of force P is:
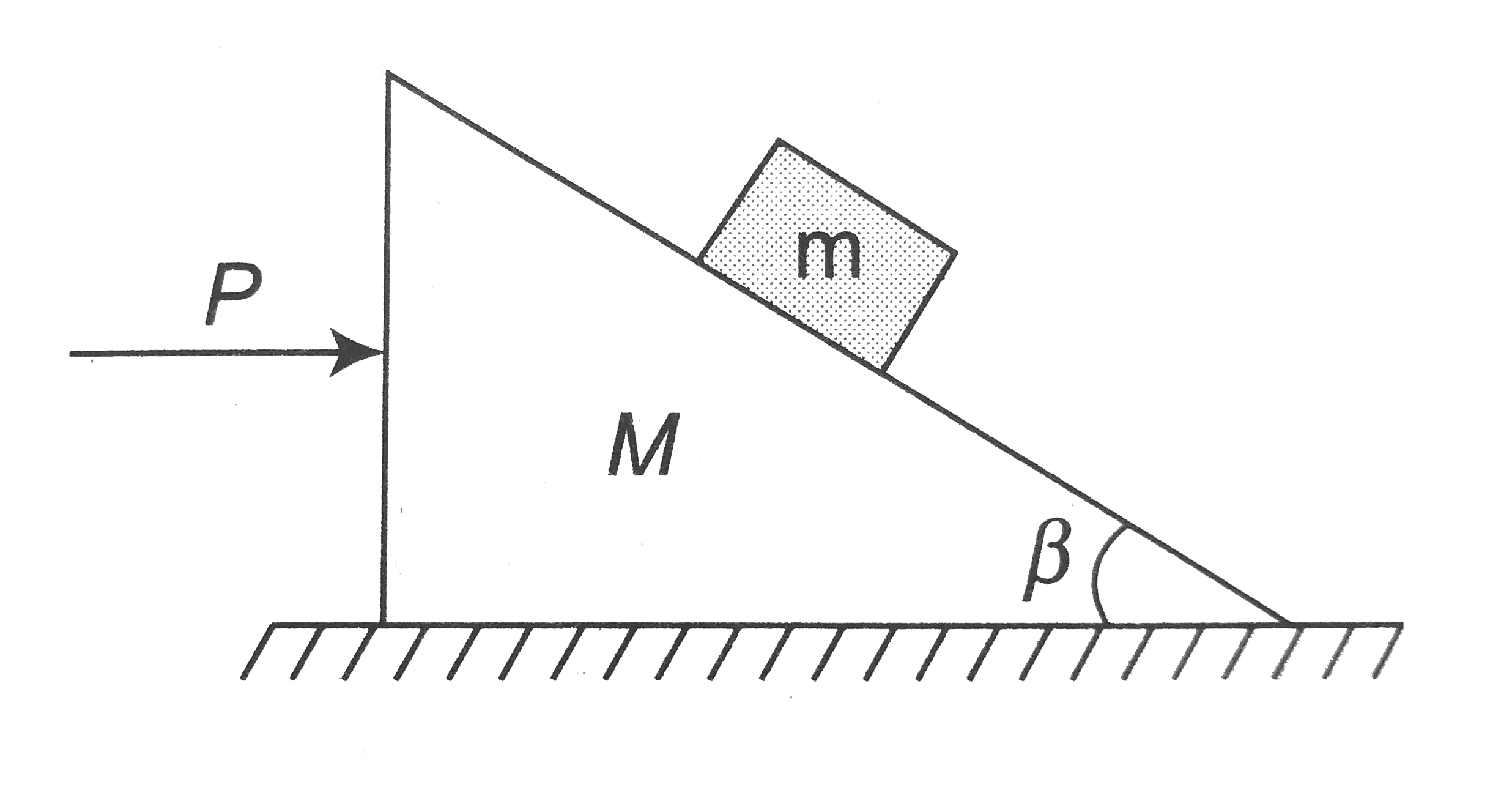 A(M+m)gtanβBgtanβCmgcosβD(M+m)gcosesβ
A(M+m)gtanβBgtanβCmgcosβD(M+m)gcosesβ
Find minimum μ so that the blocks remain stationary.
View SolutionIn the adjoining figure, the coefficient of friction between wedge (of mass M) and block (of mass m) is μ.
Find the minimum horizontal force F required to keep the block stationary with respect to wedge.

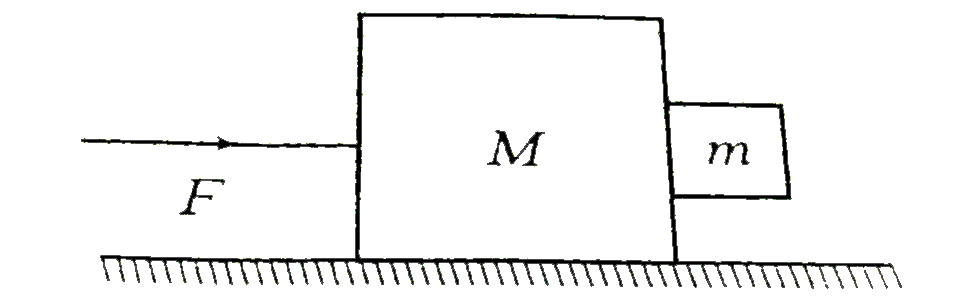
View SolutionIn the adjoining figure, the coefficient of friction between wedge ( of mass M) and block ( of mass m) is μ.
Find the minimum horizontal force F rquired to keep the block stationary with respect to wedge
View SolutionThe acceleration a of trolley so that block of mass m remains stationary with respect to rough trolley as shown in the figure, is m Trolley 0 - ...
View SolutionAs shown in the figure a block of mass 'm' is placed on a smooth wedge moving with constant acceleration such that block does not move with respect to the wedge. Find work done by the net force on the block in time t. (Initial speed is 0)
View Solution