A man wants to reach point B on the opposite bank of a river flowing at a speed as shown in figure. What minimum speed relative to water should the man have so that he can reach point B? In which direction should he swim?
Let v be the speed of boatman in still water.
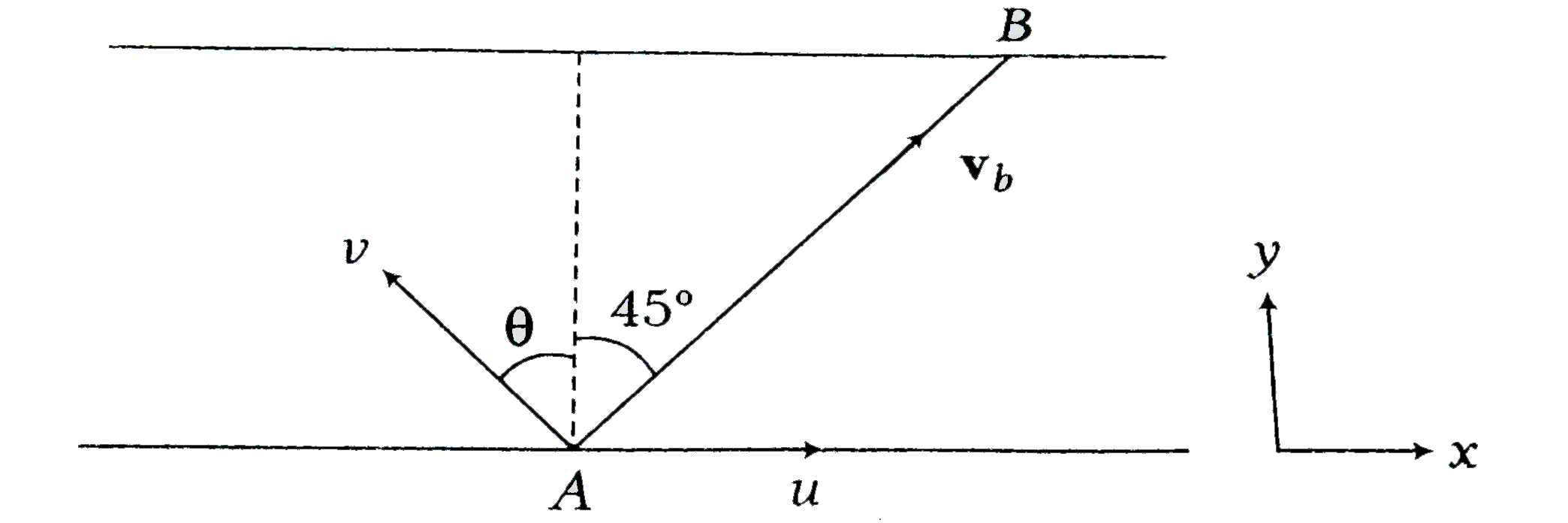
Resultant of v and u should be along AB. Components of vb (absolute velocity of boatman) along x and y direction are,
vx=u−vsinθ and vy=vcosθ
Further, tan45∘=vyvx
or 1=vcosθu−vsinθ
∴v=usinθ+cosθ=u√2sin(θ+45∘)
v is minimum at,
θ+45∘=90∘ or θ=45∘ and vmin=u√2
Topper's Solved these Questions
- MOTION IN A PLANEBook:DC PANDEYChapter:MOTION IN A PLANEExercise:Check point 3.1
Explore 10 Videos
- MOTION IN A PLANEBook:DC PANDEYChapter:MOTION IN A PLANEExercise:Check point 3.2
Explore 10 Videos
- MOTIONBook:DC PANDEYChapter:MOTIONExercise:Medical entrances gallery
Explore 19 Videos
- PROJECTILE MOTIONBook:DC PANDEYChapter:PROJECTILE MOTIONExercise:Level - 2 Subjective
Explore 10 Videos
Similar Questions
A man wants to reach point B on the opposite bank of a river flowing at a speed 4m/s as shown in the fig 1E.125 (a) what minimum speed relative to water should the man have so that he can reach point B directly by swimming? In which direction should he swin?
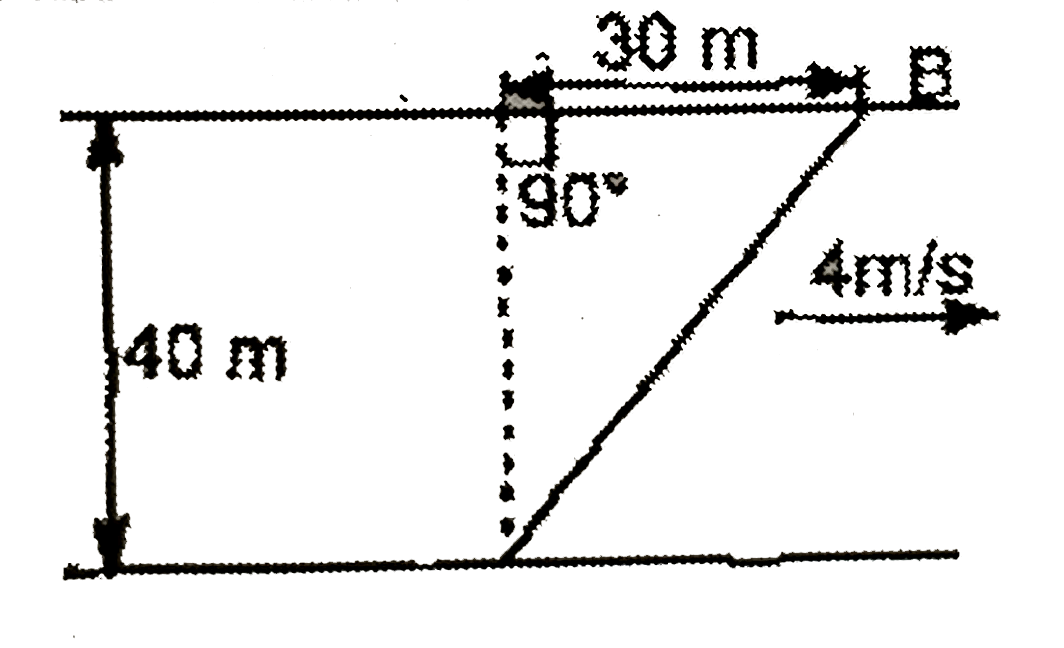
View SolutionA man wants to reach point B on the opposite bank of a river flowing at a speed u as shown in (Fig. 5.193). What minimum speed relative to water to water should the man have so that he can reach directly to point B ? In which direction should he swim ?
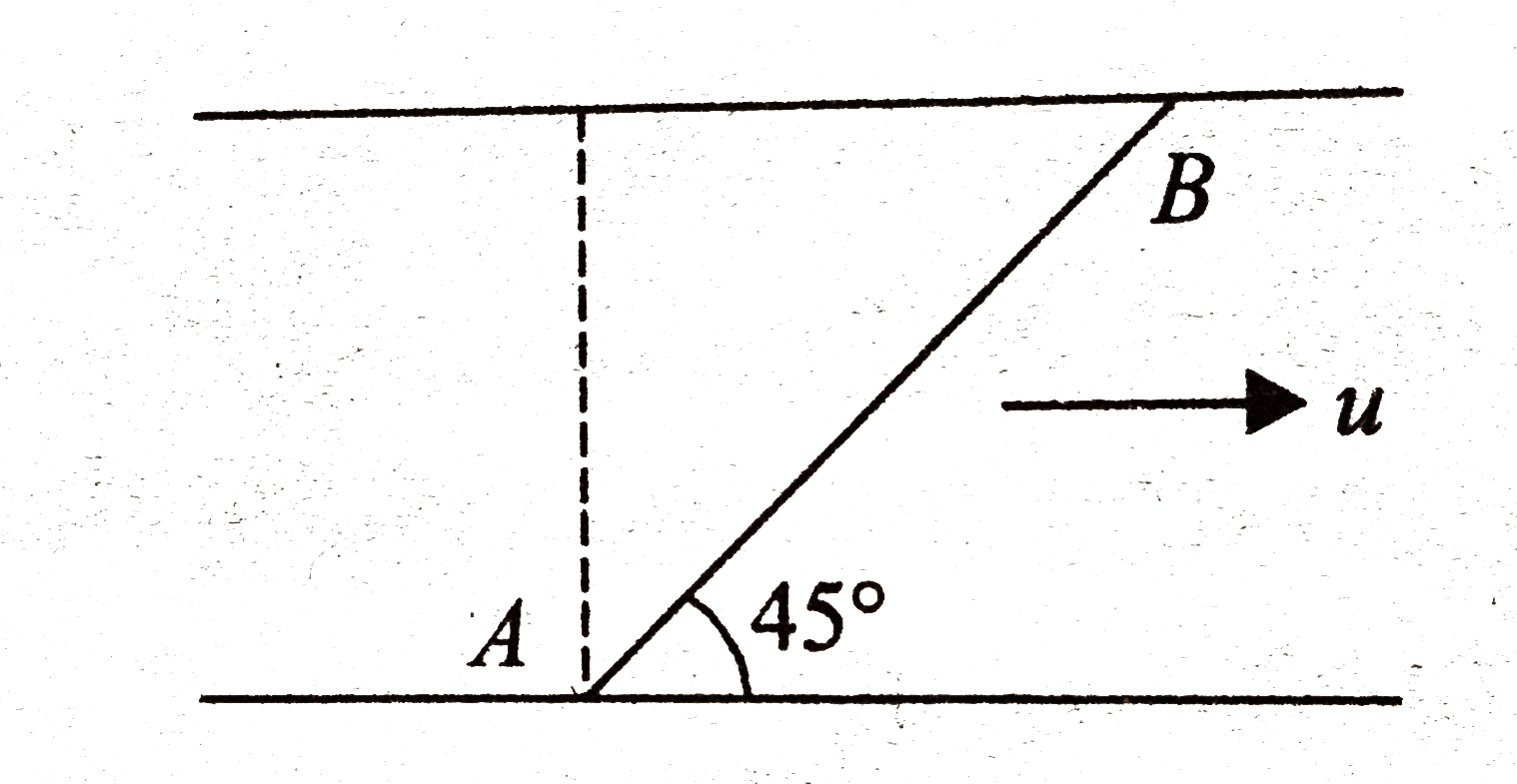 .
.
View Solution
Knowledge Check
A man wants to reach point B on the opposite bank of a river flowing at a speed 4m/s as shown in the figure. What minimum speed relative to water should the man have so that he can reach point B directly by swimming?
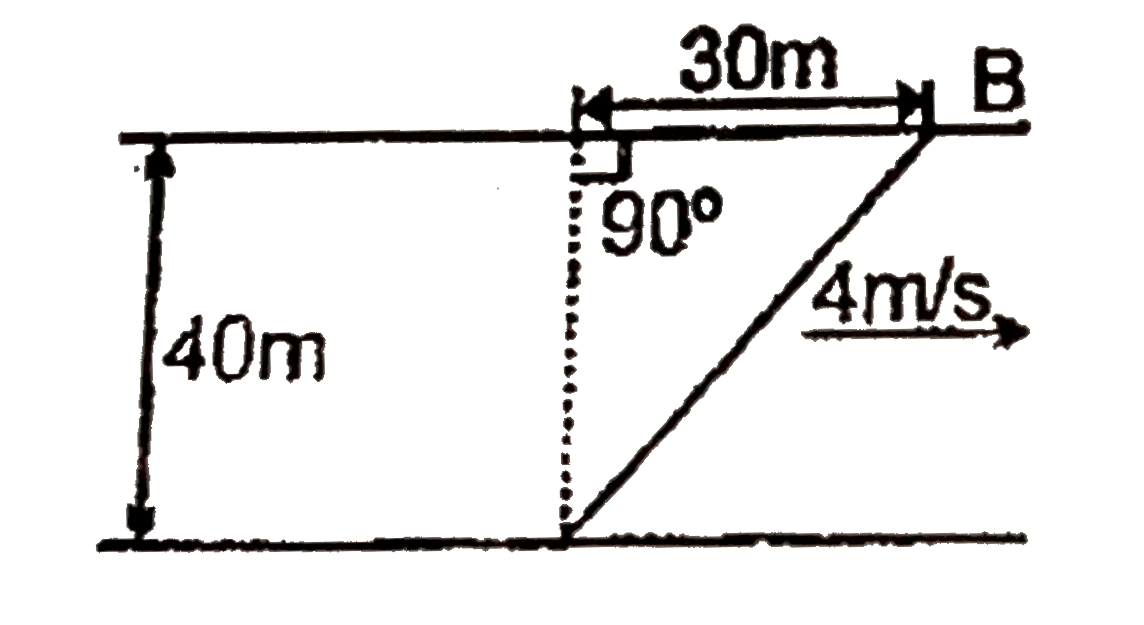 A8m/sB3.2m/sC6.5m/sD7√2m/s
A8m/sB3.2m/sC6.5m/sD7√2m/sA man in a row boat must get from point A to point B on the opposite bank of the river (see figure).The distance BC=a.The width of the river AC=b.At what minimum speed u relative to the still water should the boat travel to reach the point B?The velocity of flow of the river is v0
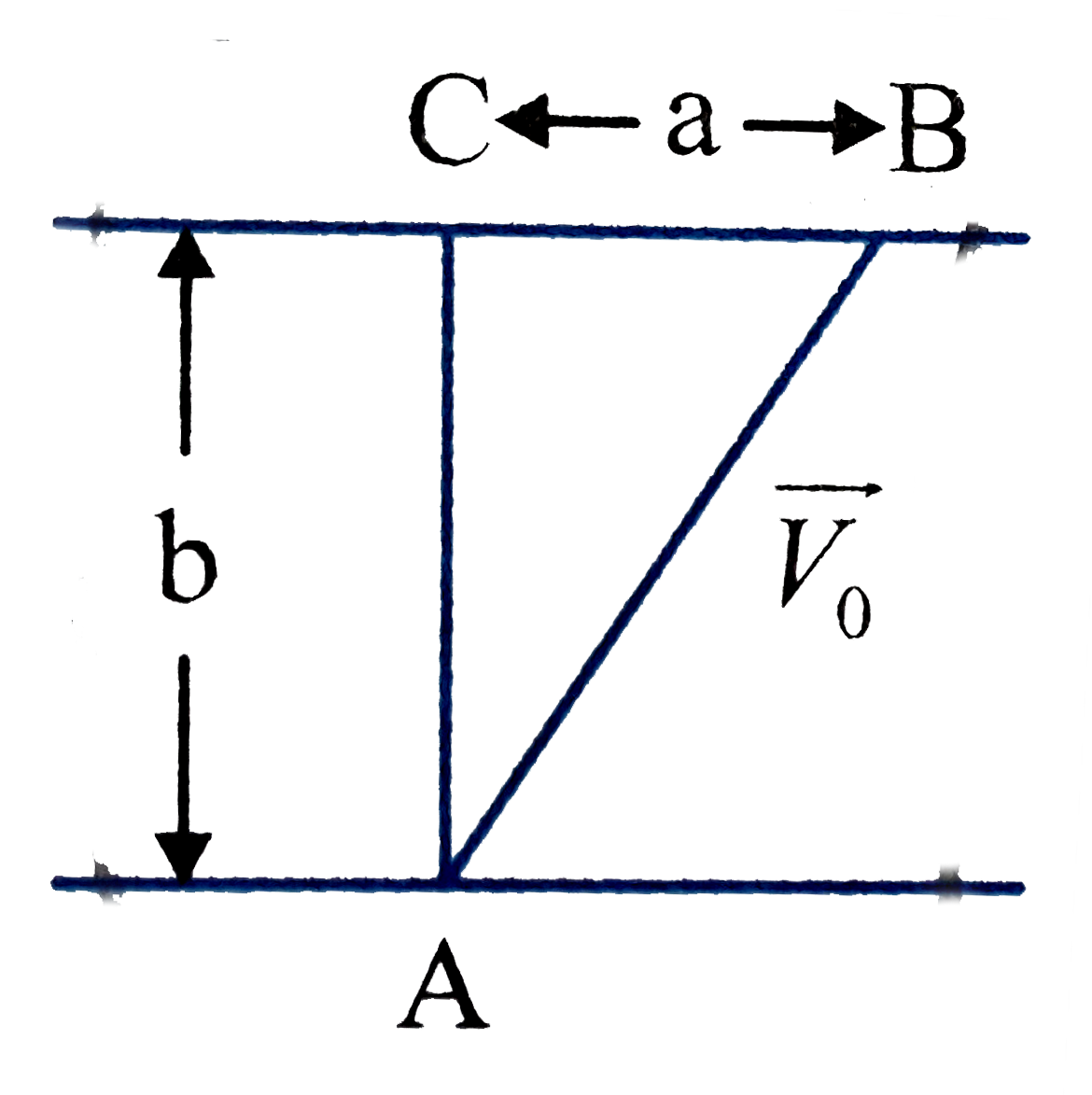 Av0b√a2+b2Bv0a√a2+b2Cv0b√2aDv0a√2b
Av0b√a2+b2Bv0a√a2+b2Cv0b√2aDv0a√2bIf a man wants to hit a target, he should point his rifle-
Ahigher than the targetBlower than the targetCin the direction of the targetDnothing can be said
A swimmer starts to swim from point a to cross a river. He wants to reach point B on the opposite side of the river. The line AB makes an angle 60∘ with the river flow as hown. The velocity of the swimmer in still water is same as that of the water

(i) In what direction should he try to direct his velocity ? Calculate angle between his velocity anf river velocity.
(ii) Find the ratio of the time taken to cross the river in this situation to the minimum time in which he can cross this river.
View SolutionA swimmer starts to swim from point a to cross a river. He wants to reach point B on the opposite side of the river. The line AB makes an angle 60∘ with the river flow as shown. The velocity of the swimmer in still water is same as that of the water
(i) In what direction should he try to direct his velocity ? Calculate angle between his velocity ? Calculate angle between his velocity and river velocity.
(ii) Find the ratio of the time taken to cross the river in this situation to the minimum time in which he can cross this river.

View SolutionA man can swim at the rate of 5kmh−1 in still water. A 1−km wide river flows at the rate of 3kmh−1 The man wishes to swim across the river directly opposite to the starting point.
(a) Along what direction must the man swim ?
(b) What should be his resultant velocity ?
( c) How much time will he take to cross the river ?
View SolutionA man swims from a point A on the bank of a river if width 100m. When he swims perpendicular to the water current, he reaches the other bank 50m downstream. The angle to the bank at which he should swim, to reach the directly opposite point B on the other bank is.
 .
.
View SolutionA man can swim in still water with a speed of 2ms−1. If he wants to cross a river of water current speed √3ms−1 along the shortest possible path, then in which direction should he swim ?
View Solution
