The pobability distribution of a discrete random variable X is given below. If
, then
Solution in Telugu
The correct Answer is:C
Step by step video, text & image solution for The pobability distribution of a discrete random variable X is given below. If E(X^(2))=Sigma x^(2)P(X=x), then 6E(X^(2))-Var(X)= {:(X=x,-1,0,1,2,),(P(X=x),1/3,1/6,1/6,1/3,):} by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
If f:R→R,g:R→R are defined by f(x)=5x−3,g(x)=x2+3, then (gof−1)(3)=
View SolutionMatch the following

The correct answer is
View SolutionIf mandσ2 are the mean and variance of the random variable X, whose distribution is given by:
X=x:0123P(X=x):1312016
View SolutionSuppose that a random variable X follows Poisson distribution . If P(X=1)=P(X=2)then P(X=5)=
View SolutionIf a random variable X follows a poisson distribution such that P(X=1)=3P(X=2), then P(x=3)=
View SolutionThe probability distribution of a discrete random variable x is given by
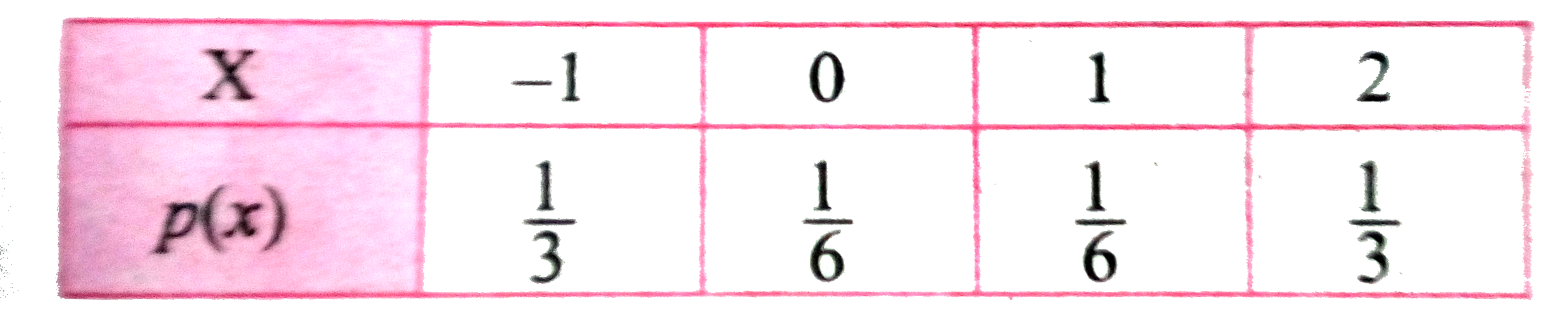
The value 6E(X2)−Var(x) is
View SolutionLet 'X' be a discrete random variable. The probability distribution of X is given below :
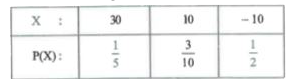
Then E(X) is equal to :
View SolutionLet 'X' be a discrete random variable. The probability distribution of X is given below :
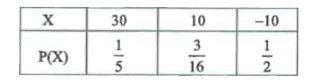
Then E(X) is equal to:
View SolutionThe variance of the random variable X having the following distribution is X=x:−2−1012P(X=x):1616131616
View SolutionThe probability distribution of a discrete random variable X is given below: X: 2 3 4 5 P(X):5k 7k 9k 11k The value of E(X) is
View Solutionकिसी यादृच्छिक चर X का प्रायिकता बंटन नीचे दिया है।
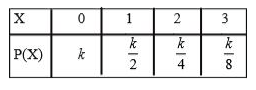
P(X≤2) तथा P(X>2) निर्धारित कीजिए
View SolutionTwo probability distributions of the discrete random variables X and Y are given below.

Prove that E(Y2)=2E(X).
View SolutionThe probability distribution of a discrete random variable X is given by
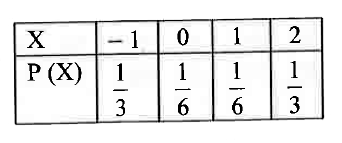
Then, the value of 6E(X2)−Var(X)is
View SolutionLet pmf of a random variable X is P(x)=3−x10,x=-1,0,1,2.=0,otherwise.Then E(x) is…
View SolutionLet X be a discrete random variable. The probability distribution of X is given below : Then E(X) equal to
View Solution

