The density inside a solid sphere of radius r varies as ρ(r)=ρ0(rR)β, where ρ0andβ are constants and r is the distance from the centre. Let E1andE2 be gravitational fields due to sphere at distance R2 and 2R from the centre of sphere. If E2E1=4, teh value of β is Solution in Telugu
2
2.5
3
4
The correct Answer is:C
Nass endclosed in a sphere of radius r is
Mr=∫ρdV=r∫0ρ0(rR)β.4πr2dr
=[4πρ0Rβ.rβ+3β+3]r0
So, mass enclosed in a sphere of radius R2 is
M1=4πρ0Rβ(R2)β+3(β+3)=4πρ0R3(β+3)×12β+3
and mass enclosed in radius R is
M2=4πρ0Rβ.Rβ+3β+3=4πρ0R3β+3
So, gravitational field intensities are
E1=GM1(R2)2=4GR2×4πρ0R3(β+3)×12β+3
and E2=GM2(2R)2=G4R2×4πρ0R3β+3
As E2E1=4, we get
G4R2×4πρ0R3β+34GR2×4πρ0R3β+3×12β+3=4
⇒2β+316=4⇒2β+3=64
2β.23=26⇒2β=8⇒2β=23⇒β=3
Topper's Solved these Questions
Similar Questions
If A represents density, B represents velocity, C represents specific heat capacity and D represents wavelength, then the quantity having the dimensions of product of A, B, C and D is
View SolutionMatch the entries in List I with those in List II.

View SolutionA non-homogenous sphere of radius R has the following density variation.
ρ=ρ0,r≤r/3,
ρ=ρ0/2,R3<r≤3R4,
ρ=ρ08,(3R)/(4)<r≤R,
What is the gravitational field due to sphere at distance 2R from center?
View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0(1−ra), where ρ0 is the density at the surface and r denotes the distance from the centre. Find the gravitational field due to this sphere at a distance 2a from its centre.
View SolutionThe volume charge density inside of sphere of radius R is given by ρ=ρ0(1−rR) ,where ρ0 is constant and r distance from centre.
(a) Find total charge Q inside sphere.
Electric field outside sphere at distance r from centre.
(b) Electric field outside sphere at distance r from centre.
(c) Electric field inside sphere at distance r from centre.
(d) At what distance from centre electric field is maximum and its value?
(e ) Sketch E versus r graph.
View SolutionA time varying magnetic field B=krt (where k is a constant r is the radial distance from centre O) is existing in a circular region of radius R as shown. If induced electric field at r=(R)/(2) is E_(1) and at r=2R is E_(2) then the ratio (E_(2))/(E_(1)) is
View SolutionA non-homogeneous sphere of radius R has the following density variation : rho{{:(rho_(0),rleR//3),(rho_(0)//2,(R//3) lt r le (3R//4)),(rho_(0)//8,(3R//4) lt r le R):} The gravitational field at a distance 2R from the centre of the sphere is
View SolutionA non-conducting solid sphere has volume charge density that varies as rho=rho_(0) r, where rho_(0) is a constant and r is distance from centre. Find out electric field intensities at following positions. (i) r lt R" " (ii) r ge R
View SolutionA solid sphere of radius R has a volume charge density ρ=ρ0r2 (where ρ0 is a constant ans r is the distance from centre). At a distance x from its centre (for x<R), the electric field is directly proportional to :
View SolutionThe density of a solid sphere of radius R is ρ(r)=20r2R2 where r is the distance from is center. If the gravitational field due to this sphere at a distance 4 R from its center is E and G is the gravitational constant, the ratio EGR is
View SolutionThe volume charge density in a spherical ball of radius R varies with distance r from the centre s ρ(r)=ρ0[1−(rR)3] where ρ0 is a constant. The radius at which the field be maximum is
View SolutionCharges Q,2Q and 4Q are uniformly distributed in three solid spheres 1,2 and 3 of radii R/2. R and 2R respectively, as shown in Fig.If magnitude of the electric fields at point P at a distance R from the centre of sphere 1,2 and 3are E1,E2 and E3 respectively, then
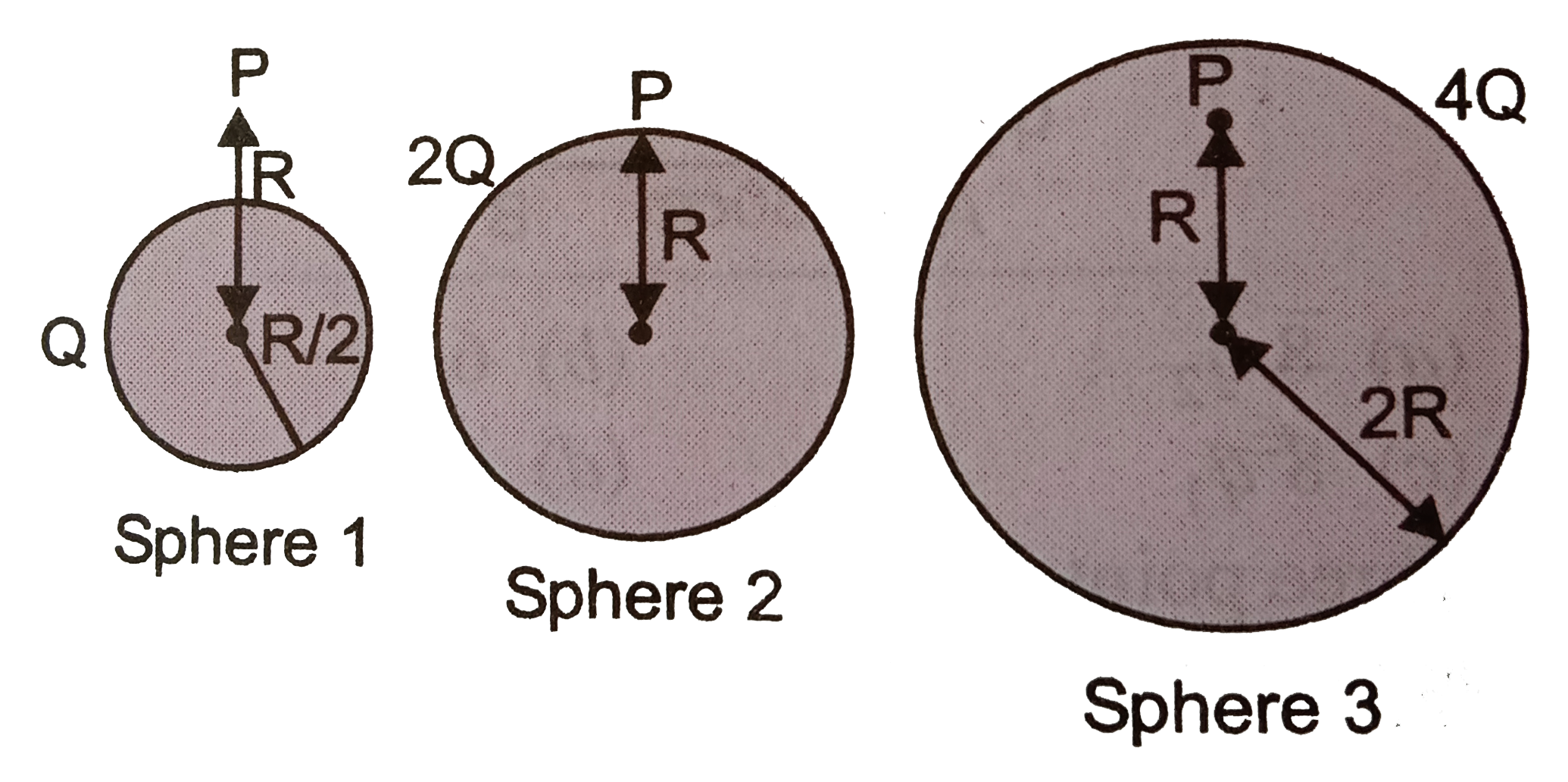
View SolutionCharge density of a sphere of radius R is rho = rho_0/r where r is distance from centre of sphere.Total charge of sphere will be
View SolutionA solid sphere of radius R has a mass distributed in its volume of mass density rho=rho_(0) r, where rho_(0) is constant and r is distance from centre. Then moment of inertia about its diameter is
View SolutionA solid sphere of density ρ=ρ0(1−r2R2),0<r≤R just floats in a liquid, then the density of the liquid is (r is the distance from the centre of the sphere)
View Solution
