A: There are 4 letters and 4 addressed envelopes. If the letters are put in the random in the envelopes , the probability that all the letters may be placed in wrongly addressed envelopes is 3/8.
R: If n letters are put at random in the n addressed envelopes , the probability that all the letters may be in wrong envelopes = 1-11!+12!−13!+.....+(−1)nn!Solution in Telugu
Both A and R are true and R is the correct explanation of A.
Both A and R are true is not correct explanation of A.
A is true but R is false
A is false but R is true
The correct Answer is:A
Step by step video, text & image solution for A: There are 4 letters and 4 addressed envelopes. If the letters are put in the random in the envelopes , the probability that all the letters may be placed in wrongly addressed envelopes is 3//8. R: If n letters are put at random in the n addressed envelopes , the probability that all the letters may be in wrong envelopes = 1-(1)/(1!) +(1)/(2!)-(1)/(3!)+.....+((-1)^(n))/(n!) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROBABILITYBook:DIPTI PUBLICATION ( AP EAMET)Chapter:PROBABILITYExercise:EXERCISE 2 (SPECIAL TYPE QUESTIONS) SET-3
Explore 9 Videos
- PERMUTATIONS & COMBINATIONSBook:DIPTI PUBLICATION ( AP EAMET)Chapter:PERMUTATIONS & COMBINATIONSExercise:EXERCISE 2 ( SPECIAL TYPE QUESTIONS ) SET -4
Explore 10 Videos
- PRODUCTS OF VECTORSBook:DIPTI PUBLICATION ( AP EAMET)Chapter:PRODUCTS OF VECTORSExercise:Exercise 2 (Special Type Questions) SET -D
Explore 14 Videos
Similar Questions
Match the following
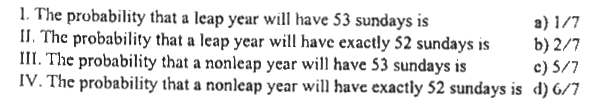
View SolutionA : the number of ways in which 5 boys and 3 girls can sit in a row so that two girls come together is 5!6P5
R : the number of ways of ways in which m ( first type of different ) things and n ( second type of different ) things (m+1≥n) can be arranged in a row so that no two things of second kind come together is m! (m+1)Pn
View SolutionA : Angle between the vectors I - 2j + k, 2i - j - k is π3.
R : If θ is the angle between a,b then cos θ=a.b|a||b|
View Solutionn letters are written to n different persons and addresses on the n envelopes are also written. If the letters are placed in the envelopes at random,the probability that at least one letter is not placed in the right envelope,is (A) 1-(1)/(n) (B) 1-(1)/(2n) (C) 1-(1)/(n^(2))(D)1-(1)/(n!)
View SolutionA person write 4 letters and addresses 4 envelopes. If the letters are placed in the envelopes at random, then the probability that all letters are not placed in the right envelopes, is a. 1/4 b. 11/24 c. 15/24 d. 23/24
View Solutionn पत्र तथा n पते लिफाफे है । सभी पत्रों की सही लिफाफों में न रखे जाने की प्रायिकता है|
View SolutionThere are 6 letters and 6 addressed envelopes . If the letters are put at random in the envelopes , the probability that all the letters may be placed in wrongly addressed envelopes is
View SolutionThere are 5 letters and 5 addressed envelopes. If the letters are put at random in the envelopes, the probability that atleast one letter may be placed in wrongly addressed envelope is
View SolutionThere are 5 letters and 5 addressed envelopes. If the letters are put at random in the envelopes , the probability that all the letters may be placed in wrongly addressed envelopes is
View Solution5 पत्र तथा 5 पते लिलखे लिफाफे है। यदि यादृच्छया पत्रों को लिफाफे में रखा जाए, तो 3 पत्रों को सही लिफाफे में रखे जाने की प्रायिकता क्या होगी?
View SolutionIf n letters are placed at random in n addressed envelops then the probability that all the letters are placed in correct envelops is
View SolutionThere are n letters and n addressed envelopes. Find the probability that all the letters are not kept in the right envelope.
View SolutionThere are n letters and n addressed envelopes. Find the probability that all the letters are not kept in the right envelope.
View SolutionA person write 4 letters and addresses 4 envelopes. If the letters are placed in the envelopes at random, then the probability that all letters are not placed in the right envelopes, is a. 1/4 b. 11/24 c. 15/24 d. 23/24
View SolutionA person write 4 letters and addresses 4 envelopes. If the letters are placed in the envelopes at random, then the probability that all letters are not placed in the right envelopes, is a. 1/4 b. 11/24 c. 15/24 d. 23/24
View Solution

