If x=(2t2),y=t3−1, then d2ydx2=Solution in Telugu
15t2
1516t2
15t716
16t2
The correct Answer is:C
Step by step video, text & image solution for If x = (2/ t ^(2)), y = t ^(3) -1, then (d ^(2) y)/(dx ^(2))= by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIFFERENTIATION Book:DIPTI PUBLICATION ( AP EAMET)Chapter:DIFFERENTIATION Exercise:SET-2
Explore 4 Videos
- DIFFERENTIATION Book:DIPTI PUBLICATION ( AP EAMET)Chapter:DIFFERENTIATION Exercise:SET-3
Explore 5 Videos
- DIFFERENTIATION Book:DIPTI PUBLICATION ( AP EAMET)Chapter:DIFFERENTIATION Exercise:EXERCISE 1C
Explore 3 Videos
- DIFFERENTIAL EQUATIONSBook:DIPTI PUBLICATION ( AP EAMET)Chapter:DIFFERENTIAL EQUATIONSExercise:Exercise 2
Explore 15 Videos
- DIRECTION COSINES AND DIRECTION RATIOSBook:DIPTI PUBLICATION ( AP EAMET)Chapter:DIRECTION COSINES AND DIRECTION RATIOSExercise:EXERCISE 2 SET -2
Explore 3 Videos
Similar Questions
1.ifF(X)=1xthenf'(1)=A2.Iff(x)=x+1x+3thenf'(−1)=B3.Iff(x)=x2thenf'(1)=C4.Iff(x)=logxthenf'(3)=D
The ascending order of A,B,C ,D is
View SolutionMatch the following
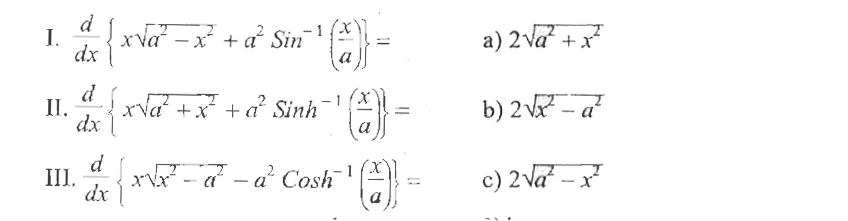
View SolutionThe function y=Sin−1(cosx) is not differentiable at
View SolutionI: The differential equation for the family of curves x2+y2−2ay=0, where a is an arbitraryconstantis (x2−y2)y'=2xy
II : The differential equation of the family of parabolas having vertices at the origin and foction y-axis is dydx=2yx
View SolutionIf the d.c.'s are (l, m, n) whose d.r's of a ray are (3, -4, 12) then ascending order of l, m, n is
View SolutionIf x2+y2=t−1tandx4+y4=t2+1t2, then x3ydydx= (a) 0 (b) 1(c) −1 (d) non of these
View Solutionif x=log_(e)t,t>0 and y+1=t^(2) then (d^(2)y)/(dx^(2))
View SolutionIf x^(3)+y^(3)=t-(1)/(t) and x^(6)+y^(6)=t^(2)+(1)/(t^(2)) then prove that (d^(2)y)/(dx^(2))=(2y)/(x^(2))
View SolutionIf x=t+1t,y=t−1t, where t≠0, then: d2ydx2=
View SolutionIf x=t2 and y=t3+1, then d2ydx2 is
View SolutionIf x=sint and y=sin3t, then d2ydx2 at t=π2 is
View SolutionIf t is a parameter and x=t+1t,y=t−1t, then d2ydx2=
View SolutionIf t is a parameter and x=t+1t,y=t−1t, then d2ydx2=
View SolutionIf x=t2 and y=t3+1, then d2ydx2 is
View SolutionIf x=sint and y=sin3t, then d2ydx2 at t=π2 is
View Solution

