किसी याद्द्च्छिक सीएचआर X का प्रायिकता बंटन P(X) निम्न है, झन k कोई संख्या है- P(X=x)=⎧⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪⎩k : यदिx=02k : यदिx=13k : यदिx=20 : अन्यथा
(i) k का मान ज्ञात कीजिये।
(ii) P(X<2),P(X≤2) तथा P(X≥2) का मान ज्ञात कीजिए।
The correct Answer is:(i) 16
(ii) 12
Step by step video, text & image solution for किसी याद्द्च्छिक सीएचआर X का प्रायिकता बंटन P(X) निम्न है, झन k कोई संख्या है- P(X=x)={(k" : "यदि x=0), (2k" : "यदि x=1), (3k" : "यदि x=2), (0" : "अन्यथा):} (i) k का मान ज्ञात कीजिये। (ii) P(X lt 2), P(X lt= 2) तथा P(X gt= 2) का मान ज्ञात कीजिए। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- प्रायिकता एवं प्रायिकता बंटनBOOK - SANJEEV PUBLICATIONCHAPTER - प्रायिकता एवं प्रायिकता बंटनEXERCISE - अन्य महत्वपूर्ण प्रश्न (वस्तुनिष्ट प्रश्न )
7 Videos
- प्रायिकता एवं प्रायिकता बंटनBOOK - SANJEEV PUBLICATIONCHAPTER - प्रायिकता एवं प्रायिकता बंटनEXERCISE - अन्य महत्वपूर्ण प्रश्न ( अतिलघुतरात्मक प्रश्न )
7 Videos
- प्रायिकता एवं प्रायिकता बंटनBOOK - SANJEEV PUBLICATIONCHAPTER - प्रायिकता एवं प्रायिकता बंटनEXERCISE - प्रश्नमाला 16.5
13 Videos
- प्रश्नपत्र BOOK - SANJEEV PUBLICATIONCHAPTER - प्रश्नपत्र EXERCISE - खण्ड- घ
2 Videos
- रैखिक प्रोग्रामन BOOK - SANJEEV PUBLICATIONCHAPTER - रैखिक प्रोग्रामन EXERCISE - अन्य महत्त्वपूर्ण प्रश्न (निबंधात्मक प्रश्न)
1 Videos
Similar Questions
एक थैले में 4 सफेद व 3 काली गेंदें हैं। दूसरे थैले में 3 सफेद व 4 काली गेंदें हैं। यदि एक गेंद उठाई जाये ओर वह काली निकले तो इस काली गेंद के दूसरे थैले से निकालने की प्रायिकता है-
View Solutionयदि P(A)=57 तथा P(B)=0, तो क्या हम P(AB) निकाल सकते हैं? यदि हाँ तो इसका मान निकालिए।
View Solutionयदि एक न्याय्य सिक्के को 10 बार उछला उछला गया तो निम्न प्रायिकताएँ ज्ञात कीजिये : (i) तथ्यत: छ: चित (ii) कम से कम छ: चित (iii) अधिकतम वीएच: चित।
View Solution∫π0xsinx1+cos2x.dxका मान ज्ञात कीजिये।
View Solutionआलेखीय विधि से निम्नलिखित रैखिक प्रोग्रामन समस्या को हल कीजिए : व्यवरोधो x+2y≤12
2x+y≤12
x+54y≥5,x≥0,y≥0 के अंतर्गत Z=60x+40y का अधिक्तमीकरण कीजिए।
View Solutionएक यादृच्छिक चार X का प्रायिकता फलन P (x) निम्न प्रकार से हे, जहाँ k कोई संख्या है
P(x)⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩kयदिx=02kयदिx=13kयदिx=20यदिअन्यथा
(a) k का मान ज्ञात कीजिए |
(b) P(X<2),P(x≤2),P(X≥2) ज्ञात कीजिए |
View Solutionयादृच्छिक चर X का प्रायिकता वितरण P(X) निम्न्वत है, जबकि k एक संख्या है |
P(X)=⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩k यदि X=02k यदि X=13k यदि X=20 अन्यथा
(i) k का मान ज्ञात कीजिए |
(ii) P(X<2),P(X≤2) व P(X≥2) के मान ज्ञात कीजिए |
View Solutionएक यादृच्छिक चर X का प्रायिकता फलन P(X) निम्न प्रकार से है, जहाँ k कोई संख्या है।
P(X)=⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩k यदि (if) X = 02k यदि (if) X = 13k यदि (if) X = 20 अन्यथा
(i) k का मान ज्ञात कीजिए
(ii) P(X<2),P(X<2),P(X≥2) ज्ञात कीजिए।
View Solutionयदि xy = 4 तथा x> 0 तो x का वह मान ज्ञात कीजिए जिसके लिए x + y न्यूनतम है।
View Solutionयदि y=1−cos2x1+cos2x है तो dydx का मान ज्ञात कीजिए।
View Solutionफलन y=f(x) के लिए यदि dydx=6(x−2)(x−3) है तो के ty अधिकतम मान के लिए का x मान ज्ञात कीजिये
View Solutionएक याद्द्च्छिक चर X का प्रायिकता बंटन नीचे दिया गया है-
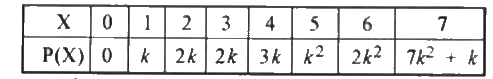ज्ञात कीजिये-
(i) k
(ii) P(X < 6)
(iii) P(X ge 6) (iv) P(0 < X <5)
View Solutionयदि A=[logx−1−logx2] और यदि det (A)=2, तब x का मान है
View Solutionएक यादृच्छिक चर X मान 0,1,2,3 ग्रहण करता है | चर X का माध्य 1.3 है | यदि P(x=3)=2P(X=1) तथा P(X=2)=0.3 हो , तो P(X=0)है |
View Solutionयदि समीकरण x2+x+1=0 के मूल a,b हैं तथा x2+px+q=0 के मूल हैं, ab,ba तो p+q का मान है
View Solutionयदि P(A) =P(B) =x और P(A∩B)=P(A'∩B')=13, तब x का मान है
View Solution