निम्नलिखित असमिकाओं की ज्यामिति या किसी अन्य विधि द्वारा स्थापना कीजिएः
a. ∣∣→a+→b∣∣≤|→a|+∣∣→b∣∣
b. ∣∣→a+→b∣∣≥||→a|−|→b∣∣∣
c. ∣∣→a−→b∣∣≤|→a|+∣∣→b∣∣
d. ∣∣→a−→b∣∣≥||→a|−|→b∣∣∣
इनमें समिका (समता) का चिन्ह कब लागू होता है?
दो सदिशों →a और →b पर विचार करते हैं जो कि समांतर चतुर्भुज OPSQ की भुजा −−→OP और −−→OQ द्वारा निरूपित होते हैं। समान्तर चतुर्भुज के योग सदिश नियम से (→a+→b) को −−→OS सदिश द्वारा निरूपित किया गया है।
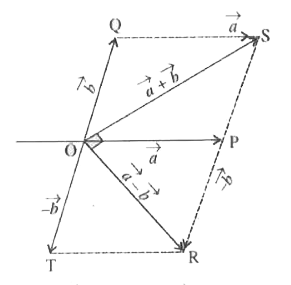
चित्र से OP=|→a|,OQ=PS=∣∣→b∣∣
और OS=∣∣→a+→b∣∣
a. सिद्ध करना है ∣∣→a+→b∣∣≤|→a|+∣∣→b∣∣
प्रमाण- हम जानते हैं कि किसी त्रिभुज में एक भुजा की लम्बाई सदैव शेष रही दो भुजाओं की लम्बाई के योग से कम होती है।
इसलिए ΔOPS में
OS<OP+PS
या OS<OP+OQ
या ∣∣→a+→b∣∣<|→a|+∣∣→b∣∣……….1
यदि दोनों सदिश एक ही सरल रेखा के अनुदिश एक ही दिशा में कार्य कर रहे हैं। अर्थात समरैखिक हैं तब
∣∣→a+→b∣∣=|vea|+∣→∣∣…………..2
समीकरण 1 तथा 2 की शर्त को शामिल करते हुए
∣∣→a+→b∣∣≤|→a|+∣∣→b∣∣
बराबर का चिन्ह तभी लागू होता है जब सदिश समरेखीय तथा एक ही दिशा में कार्यरत हो।
b. सिद्ध करना है ∣∣→a+→b∣∣≥||→a|−|→b∣∣∣
प्रमाण- किसी त्रिभुज में एक भुजा अन्य दो भुजाओं के अंतर से अधिक होती है।
ΔOPS में
OS+PS>OP
या OS>|OP−PS|
या OS>|OP−OQ|..3
∵PS=OQ
(OP-OQ) का मापांक लिया जा चुका है। इसलिए LHS सदैव धनात्मक होगा। लेकिन RHS का मान ऋणात्मक भी हो सकता है यदि OP<PS इस प्रकार समीकरण 3 से
|→a|+→b|>||→a|−∣∣→b∣∣∣∣………4
यदि दो सदिश →a तथा →b एक ही सरल रेखा के अनुदिश विपरीत दिशा में कार्य कर रहे हैं, तब
∣∣→a+→b∣∣=||→a|−|→b∣∣∣………5
समीकरण 4 तथा 5 को शामिल करने पर
∣∣→a+→b∣∣≥||→a|−|→b∣∣∣
c. सद्धि करना है ∣∣→a−→b∣∣<|→a|+∣∣→b∣∣
प्रमाण- फिर ΔOPR में
OP=|→a|,PR=∣∣−→b∣∣=→b,OR=∣∣→a−→b∣∣
अब त्रिभुज से
OR<OP+PR
या ∣∣→a−→b+<∣∣→a|+|→b∣∣……..6
अब यदि सदिश →a व →b एक ही रेखा के अनुदिश विपरीत दिशाओं में कार्यरत है तो
∣∣→a−→b∣∣=|→a|+∣∣→b∣∣……….7
समीकरण 6 तथा 7 को शामिल करने पर
∣∣→aa−→b∣∣≤|→a|+∣∣→b∣∣
d. सिद्ध करना है ∣∣→a−→b∣∣≥||→a||−∣∣→b∣∣∣∣
चूंकि किसी भी त्रिभुज मे एक भुजा दोनों भुजाओं के अंतर से अधिक होती है अतः
ΔOPR से
OR+PR>OP
या OR>|OP−PR|
या OR>|OP−OT| ………..8
∵OT=PR
यहां पर (OP−OT) का मापांक सदैव धनात्मक ही प्राप्त होगा। इसका अर्थ यह है कि LHS का माना सदैव धनात्मक ही होगा, लेकिन RHS का मान ऋणात्मक भी हो सकता है यदि
OP<OT
तब समीकरण 8. ∣∣→a−→b∣∣>||→a|−|→b∣∣∣ ……..9
यदि दोनों सदिश व एक सरल रेखा के अनुदिश एक ही दिशा में कार्य करते हैं, तब
∣∣→a−→b∣∣−||→a|−|→b∣∣∣ ……..10
समीकरण 9 तथा 10 को शामिल करने पर
∣∣→a−→b∣∣≥||→a|−|→b∣∣∣
Topper's Solved these Questions
- समतल रेखा में गतिBOOK - SANJEEV PUBLICATIONCHAPTER - समतल रेखा में गतिEXERCISE - अन्य महत्तवपूर्ण प्रश्न (बहुचयनात्मक प्रश्न)
12 Videos
- समतल रेखा में गतिBOOK - SANJEEV PUBLICATIONCHAPTER - समतल रेखा में गतिEXERCISE - अन्य महत्तवपूर्ण प्रश्न (रिक्त स्थानों की पूर्ति कीजिएः)
1 Video
- समतल रेखा में गतिBOOK - SANJEEV PUBLICATIONCHAPTER - समतल रेखा में गतिEXERCISE - गत वर्षों की विभिन्न प्रतियोगी परीक्षाओं में पूछे गये प्रश्न
26 Videos
- मात्रक एवं मापन BOOK - SANJEEV PUBLICATIONCHAPTER - मात्रक एवं मापन EXERCISE - गत वर्षों की विभिन्न प्रतियोगी परीक्षाओं में पूछे गये प्रश्न
33 Videos
- सरल रेखा में गति BOOK - SANJEEV PUBLICATIONCHAPTER - सरल रेखा में गति EXERCISE - गत वर्षों की विभिन्न प्रतियोगी परीक्षाओं में पूछे गये प्रश्न
17 Videos
Similar Questions
यदि सदिश →A की दिशा में एकांक सदिश ˆn है तो
View Solutionनिम्नलिखित में रिक्त स्थान भरें
(i) जड़त्व आघूर्ण, प्रतिबल, विद्युतशीलता तथा चुम्बकशीलता ------------------------ राशियां है।
(ii) बल आघूर्ण, कोणीस वेगों, कोणीय संवेग वे सदिश राशियां है। जिनकी दिशा .................... पेंच नियम द्वारा तय की जाती है।
(iii)cos2α+cos2β+cos2γ=………………
(iv) तीन असमतलीय सदिशों का परिणामी सदिश ................ नहीं हो सकता है।
(v) किसी वस्तु के अधिकतम क्षैतिज परास के लिए प्रक्षेप्य कोण θ-...................... होना चाहिए।
(vi) अधिकतम ऊँचाई Hmax……………….. होती है।
(vii) एक प्रेक्षप्य का पथ ................. होता है।
(viii) प्रक्षेप्य का उड्डयन काल T=…………………..g
(ix) R त्रिज्या के एक वृत्ताकार पथ में नियत चाल से गति कर रहे कण का स्पर्श रेखीय त्वरण .............. होता है।
(x) समान परास के लिए एक पिण्ड को समान चाल से........................ दिशाओं में (कोणों पर) प्रक्षेपित किया जा सकता है।
View Solutionक्षैतिज घर्षण विहीन टेबिल के केंद्र पर स्थित खूंटी से l लंबाई की डोरी का एक सिरा बांधा गया है तथा दूसरे सिरे पर m द्रव्यमान का एक कण बांधा उसे v वेग से वृत्तीय गति करवाई जाती है कण पर केंद्र की ओर लगने वाला बल होगा (T डोरी में तनाव को दर्शाता है)
View Solutionसमीकरण P=a−t2bx में P दाब, x दूरी तथा t समय है, b की विमा होगी -
View Solutionएक बिल्ली एकसमान चाल vu से X से Y तक जाती है और एकसमान चाल vd से Y से X पर वापस आती है | इसमें उसकी औसत चाल होगी -
View SolutionFor two vectors →aand→b,→a,→b=|→a|∣∣→b∣∣ then (A) →a∣∣→b (B) →a⊥→b (C) →a=→b (D) none of these
View Solutionदर्शाइए कि दो सदिशों →a ओर →b के लिए |→a|→b+∣∣→b∣∣→a , |→a|→b−∣∣→b∣∣→a, परस्पर लम्बवत हैं
View SolutionProve that ∣∣→a×→b∣∣2=∣∣∣→a⋅→a→a⋅→b→a⋅→b→b⋅→b∣∣∣.
View Solutionदर्शाइए कि दो शून्येतर सदिशों →a और →b के लिए |→a|→b+∣∣→b∣∣→a,|→a|→b|−|→b∣→a पर लंब है।
View SolutionIf |→a|=∣∣→b∣∣, then (→a+→b).(→a−→b) is equal to
View Solutionसदिशों तथा के लिए सिद्ध कीजिए कि
∣∣→a×→b∣∣2=∣∣∣→a.→a→a.→b→a.→b→a.→b∣∣∣
View Solutionनिम्नलिखित असमिकाओं की ज्यामिति या किसी अन्य विधि द्वारा स्थापना कीजिए :
(a) ∣∣→A+→B∣∣≤∣∣→A∣∣+∣∣→B∣∣
(b) ∣∣→A+→B∣∣≥∣∣∣∣→A∣∣−∣∣→B∣∣∣
(c ) ∣∣→A−→B∣∣≤∣∣→A∣∣+∣∣→B∣∣
∣∣→A−→B∣∣≤∣∣→A∣∣+∣∣→B∣∣
∣∣→A−→B∣∣≥∣∣∣∣→A∣∣−∣∣→B∣∣∣
इनमे समिका (समता) का चिन्ह कब लागू होता है ?
View Solutionदर्शाइए कि दो शून्येतर सदिशों →a और →b के लिए |→a|→b+∣∣→b∣∣→a,|→a|→b−∣∣→b∣∣→a पर लम्ब है ।
View SolutionFind ∣∣→b∣∣,if (→a+→b).(→a−→b)=8 and |→a|=8∣∣→b∣∣.
View Solutionप्रक्कथनः यदि़ ∣∣→A+→B∣∣=∣∣→A−→B∣∣ हो तो →A तथा →B के बीच का कोण 90∘ होगा।
कारणः →A+→B=→B+→A
View SolutionFind ∣∣→b∣∣ if (→a+→b).(→a−→b)=8and|→a|=8∣∣→b∣∣
View Solution