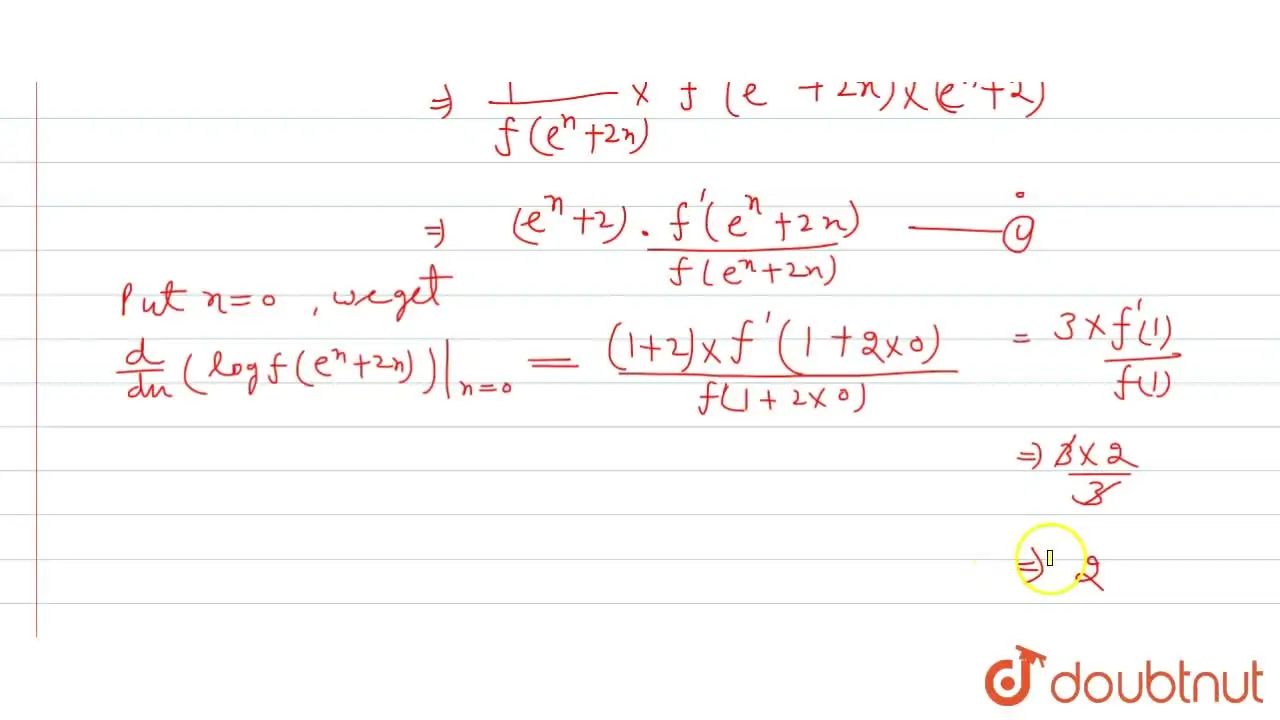If f(1)=3 , f'(1)=2 , then ddx {logf(ex+2x)} at x=0 is equal to........
Step by step video & image solution for If f(1)=3 , f'(1)=2 , then d/(dx) {logf(e^x+2x)} at x=0 is equal to........ by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
Suppose ∣∣∣f'(x)f(x)f''(x)f'(x)∣∣∣=0 where f(x) is continuous differentiable function with f'(x)≠0 and satisfies f(0)=1 and f'(0)=2, then f(x)=eλx+k, then λ+k is equal to ..........
View SolutionIf for a continuous function f,f(0)=f(1)=0,f'(1)=2andg(x)=f(ex)ef(x), then g'(0) is equal to
View SolutionIf for a continuous function f,f(0)=f(1)=0,f′(1)=2andy(x)=f(ex)ef(x) , then y′(0) is equal to a. 1 b. 2 c. 0 d. none of these
View SolutionLet f(x)=(2x−π)3+2x−cosx,T h e n ,ddx[f−1(x)] at x=π is equal to :
View SolutionIf adifferentiabl e function f(x)=ex+2x is given, then equal to ddx(f−1(x)) at x=f(ln3) is equal to
View SolutionIf f(x)=tan−1(3x−x31−3x2) then ddx(f(x)) is equal to
View SolutionIf ddx[f(x)]=11+x2, then: ddx[f(x3)]=
View SolutionIf f(x)=loge(1−x1+x),|x|<1, then f(2x1+x2) is equal to
View SolutionSuppose for a differentiable function f, f(0)=0,f(1)=1 and f'(0)=4=f'(1). If g(x)=f(ex)ef(x) then g'(0) is equal to
View Solution3f(x)−f(1x)=logex4(x>0), then f(10−x) is equal to
View Solution