The mean and standard deviation of 20 observations are found to be 10 and 2, respectively. One rechecking, it was found that an observation 8 was incorrect. Calculate the correct mean and standard deviation in each of the following cases. (i) If
Here n=20 mean ¯x=10 and standard deviation σ=2
(∑xi)=10
⇒∑xi=10×20=200
and ∑x2in−(¯x)2=σ2
⇒∑x2i20−(10)2=22
⇒∑x2i=2080
(i) If observation 8 is omitted , then
N=20−1=19
∑Xi=∑xi−8=200−8=192
and correct mean =∑xiN=19219=10.1
Now, ∑x2i=∑x2i−82=2080−64=2016
and correct standard deviation
=√∑x2iN−(¯x)2=√201619−(10.1)2=2.02
(ii) If 8 is replaced by 12,
Correct sum of 20 observations
∑xi=200−8+12=204
∴ Correct mean =20420=10.2
Now ∑x2i=2080−82+122=2160
∴ Correct standard deviation
=
⎷∑x2in−(∑xin)2=√216020−(10.2)2
=√108−104.04=√3.96=1.98
Topper's Solved these Questions
Similar Questions
The mean and standard deviation of 18 observations are found to be 7 and 4 respectively. On rechecking it was found that an observation 12 was misread as 21. Calculate the correct mean and standard deviation.
View SolutionThe mean and standard deviation of 20 observations are found to be 10 and 2, respectively. On review, it was found that an observation 8 was incorrect. Then the correct standard deviation if the wrong item is omitted is …………..
View Solution
Knowledge Check
The mean and standard deviation of 20 observations are found to be 10 and 2 respectively. On rechecking, it was found that an observation 8 was incorrect. Find the new standard deviation if wrong item is omitted.
A1.99B2.76C2.99D3.46The mean and standard deviation of 20 observations are found to be 10 and 2 . On rechecking , it was found that an observation 8 was incorrect. Find the correct standard deviation if wrong item is omitted .
A1.88B1.99C1.95DNone of theseThe mean and variance of 10 observation are found to be 10 and 4 respectively. On rechecking it was found that an observation 8 was incorrect. If it is replaced by 18, then the correct variance is
A7B8C9D556
The mean and variance of 20 observations are found to be 10 and 4. respectively. On rechecking, it was found that an observation 9 was incorrect and the correct observation was 11. Then the correct variance is
View SolutionCalculate mean and standard deviation from the following data:
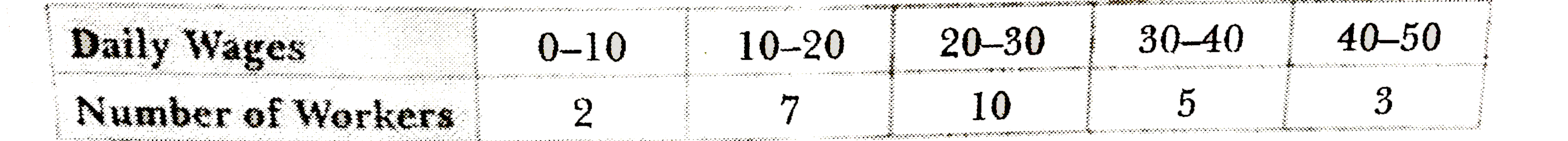
View SolutionThe mean and standard deviation of a group of 100 observations were found to be 20 and 3, respectively. Later on it was found that three observations were incorrect, which are recorded as 21,21 and 18. Find the mean and standard deviation if the incorrect observations are omitted.
View SolutionThe mean and variance of 20 observations are found to be 10 and 4 respectively. On rechecking, it was found that an observation 8 is incorrect. If the wrong observation is omitted, then the correct variance is
View SolutionThe mean and variance of 10 observations are found to be 10 and 5 respectively. On rechecking it is found that an observation 5 is incorrect. If the incorrect observation is replaced by 15, then the correct variance is
View Solution
