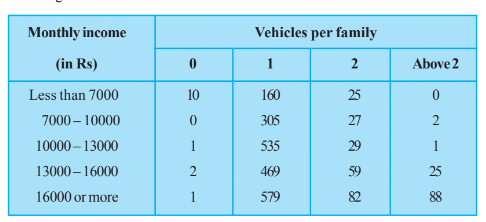
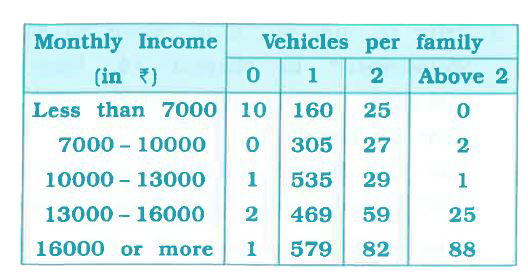
An organisation selected 2400 families at random and surveyed them to determine relationship between income level and the number of vechicles in a family. The information gathered is listed in the table below:

Suppose a family is chosen. Find the probability that the family chosen is :
(i) earning Rs. 10000-13000 per month and owning exactly 2 vehicles.
(ii) earning Rs. 16000 or more per month and owning exactly 1 vehicle.
(iii) earning less than Rs. 7000 per month and does not own any vehicle.
(iv) earning Rs. 13000-16000 per month and owning more than 2 vehicles.
(v) owning not more than 1 vehicle.
Total number of families selected by the organisation, n(S) = 2400
(i) The number of families earning Rs. 10000-13000 per month and owing exactly 2 vehicles,
n(E1)=29
∴ Required probability=n(E1)n(S)=2924000
(ii) The number of families earning Rs. 16000 or more per month and owing exactly 1 vehicle,
n(E2)=579
∴ Required probability=n(E2)n(S)=5792400
(iii)The number of families earning less than Rs. 7000 per month and does not own any vehicle,
n(E3)=10
∴ Required probaility=n(E3)n(S)=102400=1240
(iv) The number of families earning Rs. 13000-16000 per month and owing more than 2 vehicles,
n(E4)=25
∴ Required probability=n(E4)n(S)=252400=252400=196
(v) The number of families owing not more than 1 vechicle,
n(E5)=(10+1+2+1)+(160+305+535+469+579)=2062
∴ Required probability=n(E5)n(S)=20622400=10311200
Topper's Solved these Questions
- PROBABILITYBOOK - NAGEEN PRAKASHANCHAPTER - PROBABILITYEXERCISE - Exercise
12 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHANCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHANCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- POLYNOMIALSBOOK - NAGEEN PRAKASHANCHAPTER - POLYNOMIALSEXERCISE - Revision Exercise (short Answer Questions)
16 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (long Answer Questions)
5 Videos
Similar Questions
An organisation selected 2400 families at random and surveyed them to determine a relationship between income level and the number of vehicles in a family . The information gathered is listed in the table below
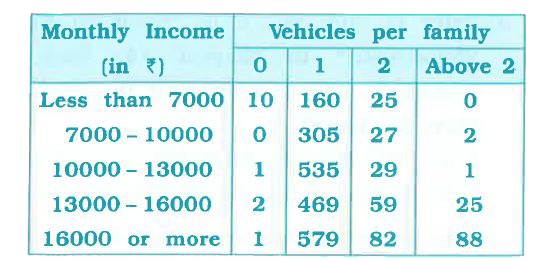
Suppose a family is chosen, Find probability that the family chosen is
earning Rs 10000 - Rs 13000 per month and owning exactly 2 vehicles.
View SolutionAn organisation selected 2400 families at random and surveyed them to determine a relationship between income level and the number of vehicles in a family. The information gathered is listed in the table below.
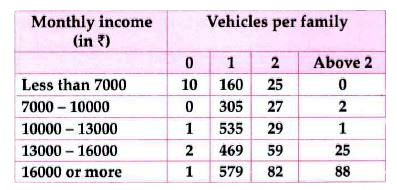
Suppose a family is chosen. Find the probability that the family chosen is
earning Rs 10000 13000 per month and owningexactly 2 vehicles.
View SolutionAn organisation selected 2400 families at random and surveyed them to determine a relationship between income level and the number of vehicles in a family. The information gathered is listed in the table below.
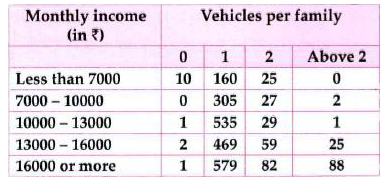
Suppose a family is chosen. Find the probability that the family chosen is
earning Rs 13000-16000 per month and owning more than 2 vehicles.
View SolutionAn organisation selected 2400 families at random and surveyed them to determine a relationship between income level and the number of vehicles in a family. The information gathered is listed in the table below.

Suppose a family is chosen. Find the probability that the family chosen is
earning Rs 16000 or more per month and owning exactly 1 vehicle.
View SolutionAn organisation selected 2400 families at random and surveyed them to determine a relationship between income level and the number of vehicles in a family . The information gathered is listed in the table below
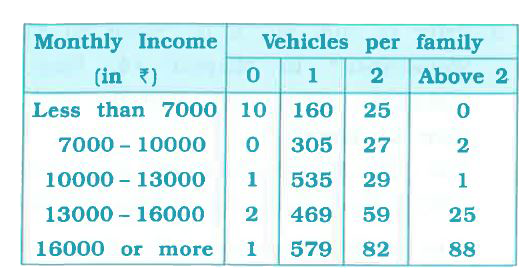
Suppose a family is chosen, Find probability that the family chosen is
earning Rs 13000 - Rs 16000 per month and owning more than 2 vehicles.
View SolutionAn organisation selected 2400 families at random and surveyed them to determine a relationship between income level and the number of vehicles in a family . The information gathered is listed in the table below
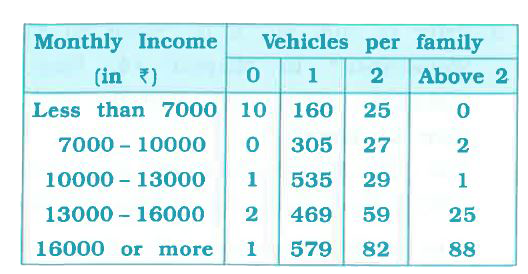
Suppose a family is chosen, Find probability that the family chosen is
earning Rs 16000 or more per month and owning exactly 1 vehicle.
View SolutionAn organisation selected 2400 families at random and surveyed them to determine a relationship between income level and the number of vehicles in a family. The information gathered is listed in the table below.
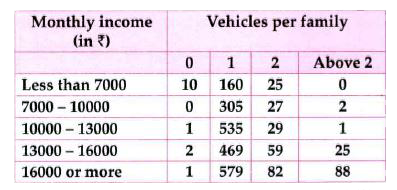
Suppose a family is chosen. Find the probability that the family chosen is
owning not more than 1 vehicle
View SolutionAn organisation selected 2400 families at random and surveyed them to determine a relationship between the income level and the number of vehicles in a family . The information gathered is listed in the table below :
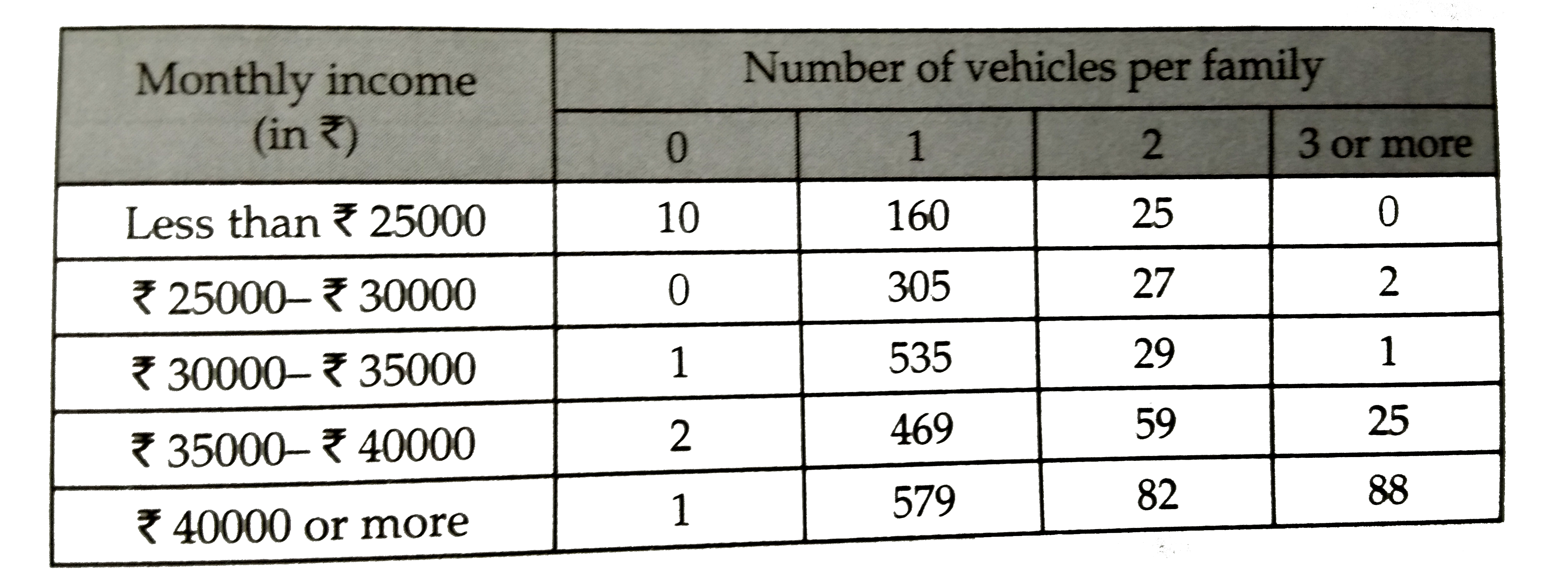
Suppose a family is chosen at random . Find the probability that the family chosen is
(i) earning ₹ 25000 - ₹ 30000 per month and owning exactly 2 vehicles .
(ii) earning ₹ 40000 or more per month and owing exactly 1 vehicle.
(iii) earning less than ₹ 25000 per month and not owing any vehicle .
(iv) earning ₹ 35000 - ₹ 40000 per month and owning 2 or more vehicles.
(v) Owing not more than 1 vehicle .
View SolutionAn organization selected 2400 families at random and surveyed them to determine a relationship between income level and the number of vehicles in a family. The information gathered is listed in the table below:
Suppose a family is chosen. Find the probability that the family chosen is (i) earning Rs 10000 – 13000 per month and owning exactly 2 vehicles. (ii) earning Rs 16000 or more per month and owning exactly 1 vehicle. (iii) earning less than Rs 7000 per month and does not own any vehicle. (iv) earning Rs 13000 – 16000 per month and owning more than 2 vehicles. (v) owning not more than 1 vehicle
View SolutionAn organisation selected 2400 families at random and surveyed them to determine a relationship between income level and the number of vehicles in a family . The information gathered is listed in the table below
Suppose a family is chosen, Find probability that the family chosen is
earning less than Rs 7000 per month and does not own any vehicle.
View Solution
