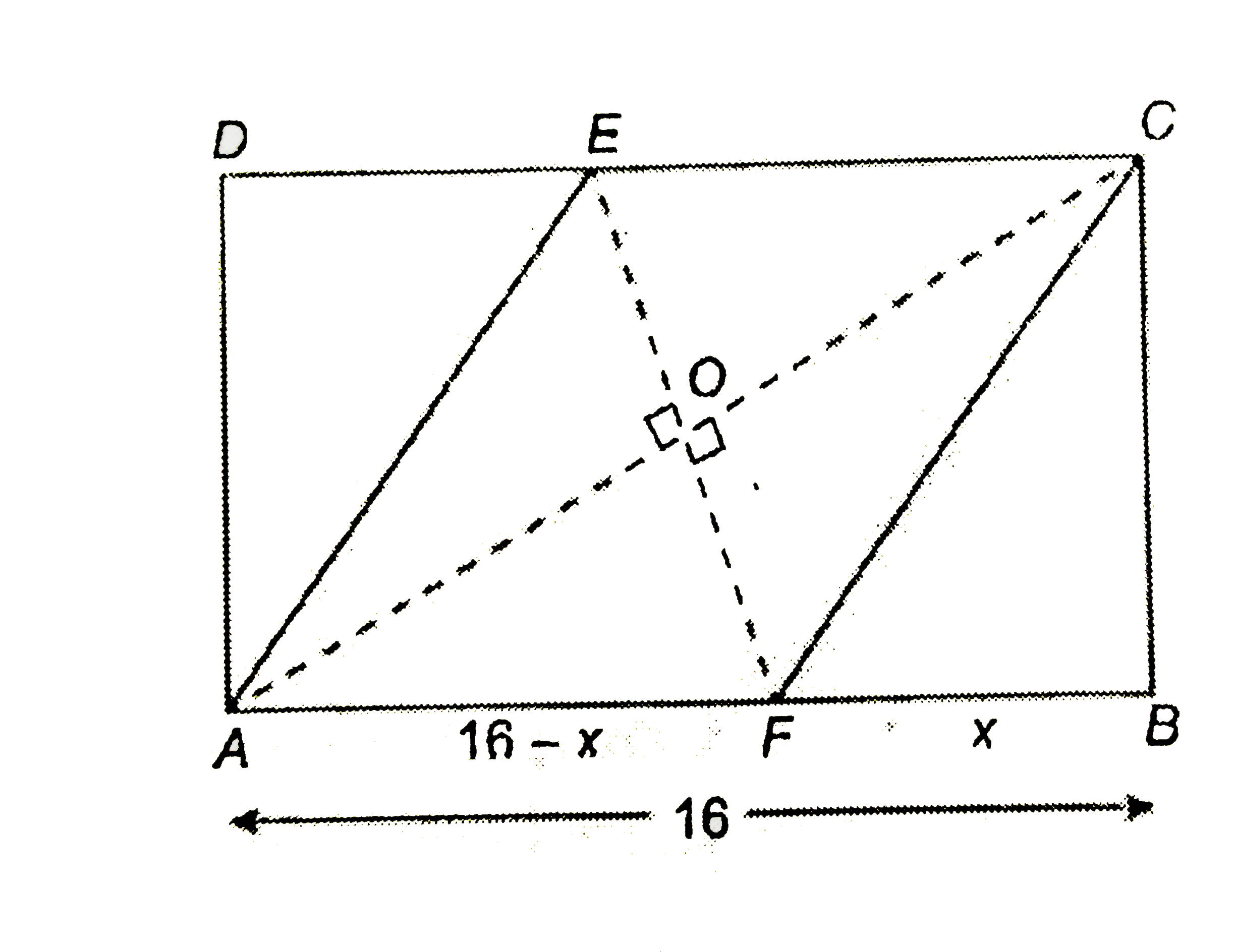
ABCD is a rectangle with AB=16 units and BC=12 units. F is a point on AB and E is a point on CD such that AFCE is a rhombus. Find the length of EF.
15 units
16 units
17 units
18 units
The correct Answer is:A
Let FB x units
∴AF=16−x units
Since AFCE is a rhombus.
∴FC=AF=16−x
Now, by Pythagoras theorem,
CF2=FB2+BC2
⇒(16−x)2=x2+144
⇒256+x2−32x=x2+144
⇒32x=112
⇒x=11232=72 units
∴ Side of rhombus =16−x=16−72=252 units
By Phythagoras theorem,
aC2=AB2+BC2
⇒AC2=(16)2+(12)2=256+144=400⇒AC=20
∴AO=12×AC=10 units
∴AE2=OE2+AO2 (by Phythagoras theorem)
(252)2=OE2+(10)2
⇒OE2=156.25−100=56.25⇒OE=7.5
∴EF=2×OE=2×7.5=15 units
Topper's Solved these Questions
- HERONS'S FORMULABook:NAGEEN PRAKASHANChapter:HERONS'S FORMULAExercise:Problems From NCERT / Exemplar
Explore 10 Videos
- HERONS'S FORMULABook:NAGEEN PRAKASHANChapter:HERONS'S FORMULAExercise:Exercise 12a
Explore 11 Videos
- CONSTRUCTIONSBook:NAGEEN PRAKASHANChapter:CONSTRUCTIONSExercise:EXAMPLE SOLUTION.
Explore 19 Videos
- INTRODUCTION TO EUCLID'S GEOMETRYBook:NAGEEN PRAKASHANChapter:INTRODUCTION TO EUCLID'S GEOMETRYExercise:Exercise
Explore 3 Videos
Similar Questions
ABCD is a rectangle where ratio of the length of AB and BC is 3 : 2. If P is the mid point of AB . Find sin ∠CPB
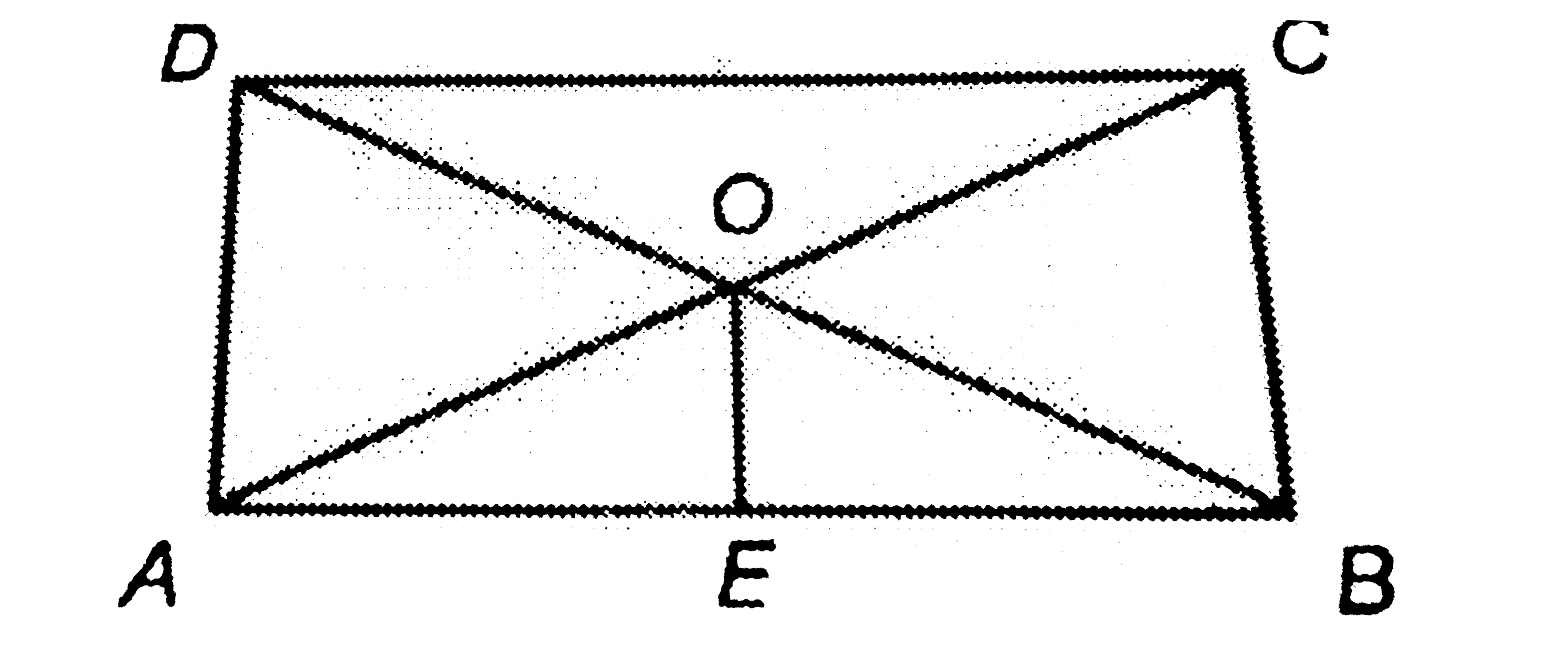
View SolutionIn the given rectangle ABCD, the sum of the lengths of two diagonals is equal to 52 cm and E is a point in AB, such that ¯¯¯¯¯¯OE is perpendicular to ¯¯¯¯¯¯AB. Find the lengths of the sides of the rectangle, if OE=5 cm.
View Solution
Knowledge Check
Diagonal AC of a rectangle ABCD is produced to the point E such that AC:CE=2:1,AB=8cm and BC=6cm. Find the length of DE.
A2√19 cmB15 cmC3√17 cmD13 cmABCD is a rectangle where ratio of the length of AB and BC is 3 : 2. If P is the mid point of AB . Find sin ∠CPB
A35B25C34D45Let ABCD be a trapezium in which AB||DC and E be the mid-point of AD. If F be a point on BC such that EF||AB. Then EF, where F is the mid-point of BC, is equal to
 AAB + DCB12(AB+DC)C13(AB+DC)DNone of these
AAB + DCB12(AB+DC)C13(AB+DC)DNone of these
Let ABCD be a rectangle such that AB=10 units and BC=8 units. Taking AB and AD as x and y axis respectively, find the coordinates of A, B, C and D.
View SolutionABCD is a rectangle and PQRS are respectively the mid points of the side AB,BC,CDand DA.T is any point of SR.If the area of ABCD is 144sq.units.Find the area of the triangle PQT.
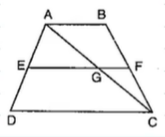
View SolutionIn the figure ABCD is a trapezium in which side AB is parallel to side DC and E is the midpoint of side AD. If F is a point on the side BC such that the line segment EF is parallel to DC.Prove that Fis the mid-point of BC and EF=12(AB+DC)
View SolutionABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionIn Figure, ABCD isa trapezium in which side AB is a parallel to side DC and E is the mid-point of side AD. If F is a point on the side BC such that the segment EF is parallel to side DC . Prove that F is the mid point of BC and EF=12(AB+DC).
View Solution

