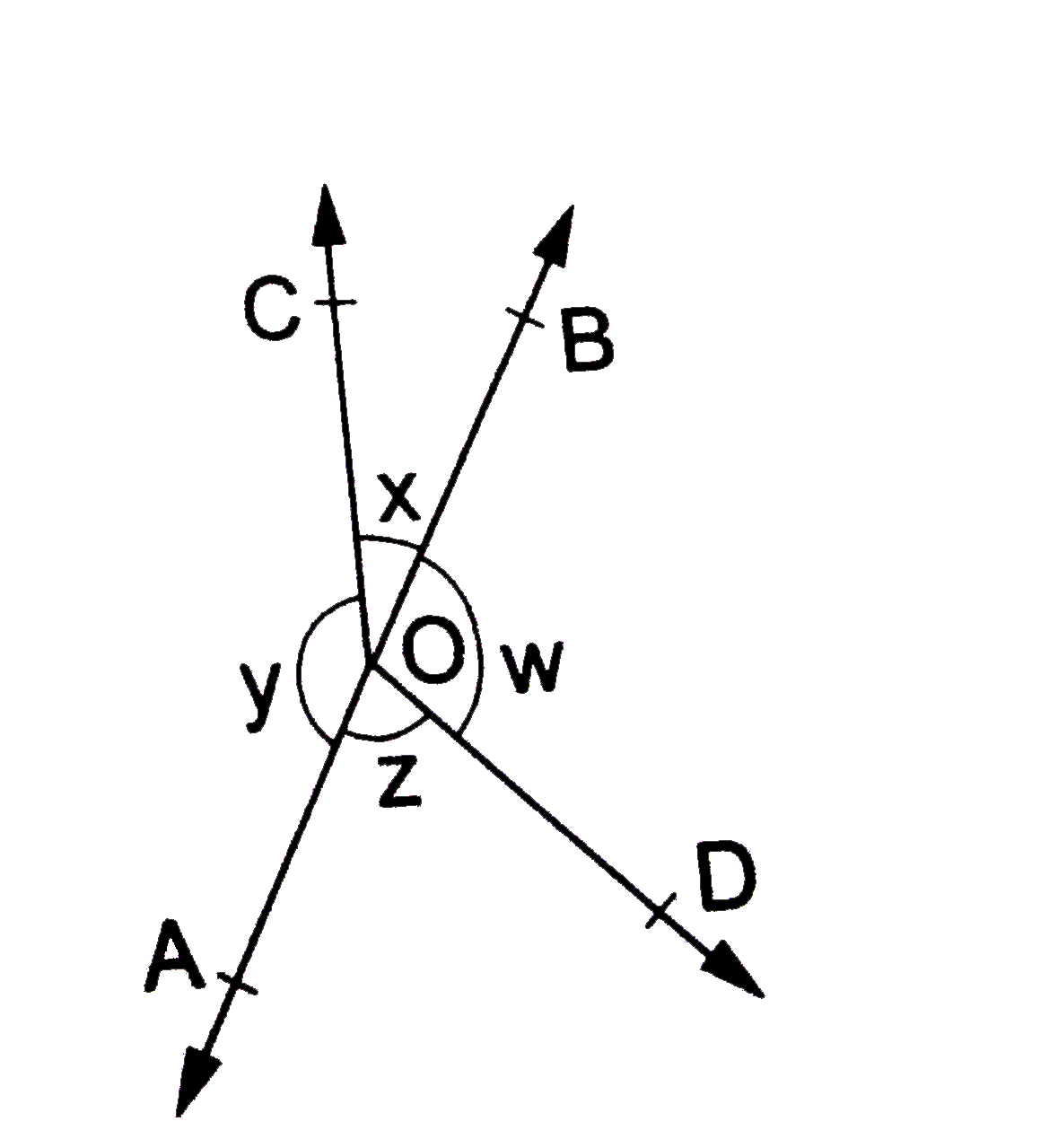
In Fig. 6.16, if x+y=w+z, then prove that AOB is a line.
x+y+w+z=360∘ (angle at a point ).....(1)
x+y=w+z (given)....(2)
x+y+x+y=360∘ [from (1) and (2)]
2(x+y)=360∘⇒x+y=180∘
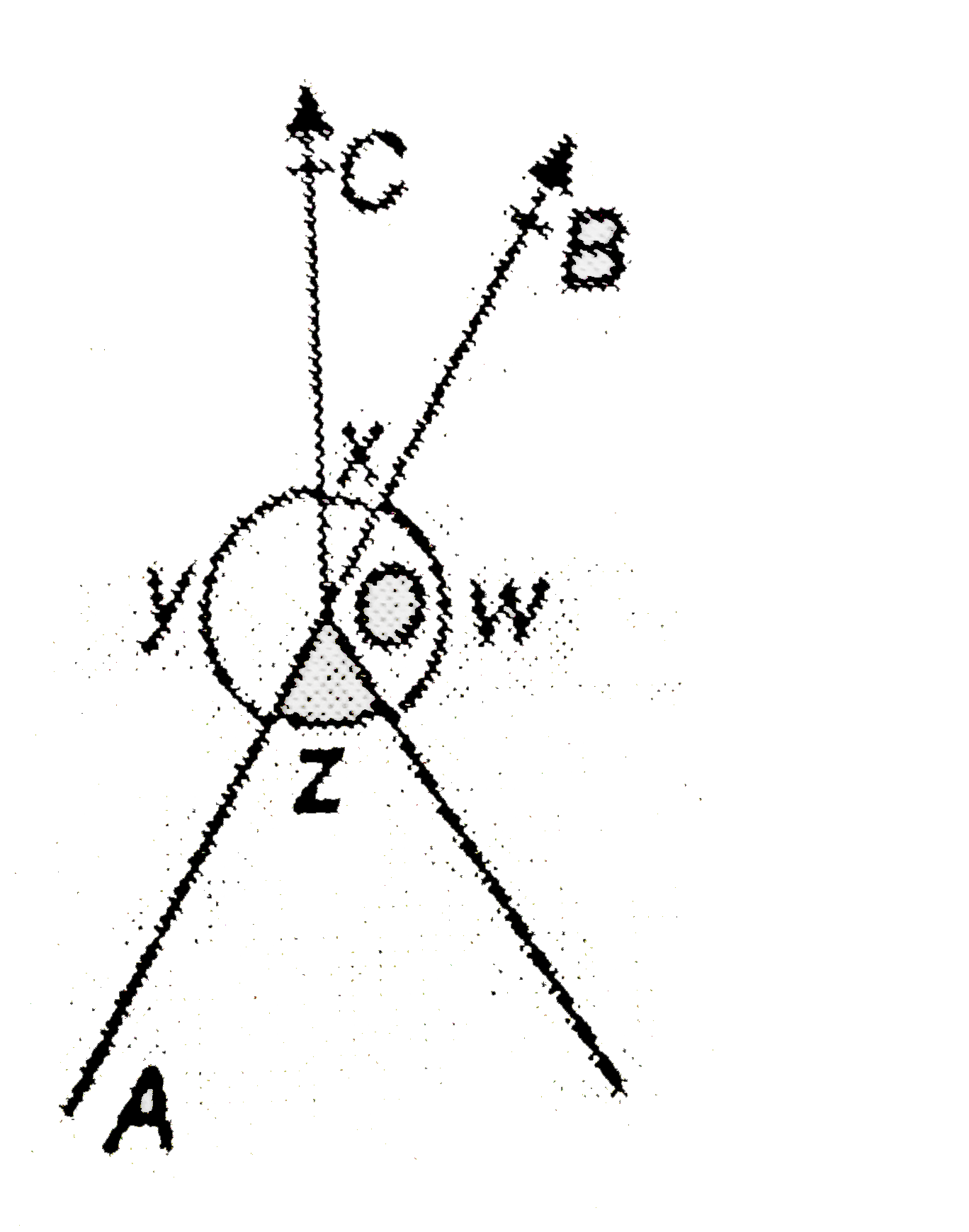
Hence, AOB is a straight line.
Topper's Solved these Questions
- LINES AND ANGLESBook:NAGEEN PRAKASHANChapter:LINES AND ANGLESExercise:Exercise 6 A
Explore 19 Videos
- LINES AND ANGLESBook:NAGEEN PRAKASHANChapter:LINES AND ANGLESExercise:Exercise 6 B
Explore 16 Videos
- LINES AND ANGLESBook:NAGEEN PRAKASHANChapter:LINES AND ANGLESExercise:Revision Exercise (long Answer Questions )
Explore 6 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBook:NAGEEN PRAKASHANChapter:LINEAR EQUATIONS IN TWO VARIABLESExercise:Revision Exercise
Explore 12 Videos
- NUMBER SYSTEMBook:NAGEEN PRAKASHANChapter:NUMBER SYSTEMExercise:Revision Exercise (short Answer Questions)
Explore 10 Videos
Similar Questions
In Figure, if x+y=w+z, then prove that AOB is a line Fig.
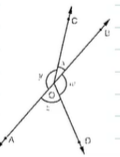
View SolutionIn Fig. 6.16, if x+y=w+z, then prove that AOB is a line.
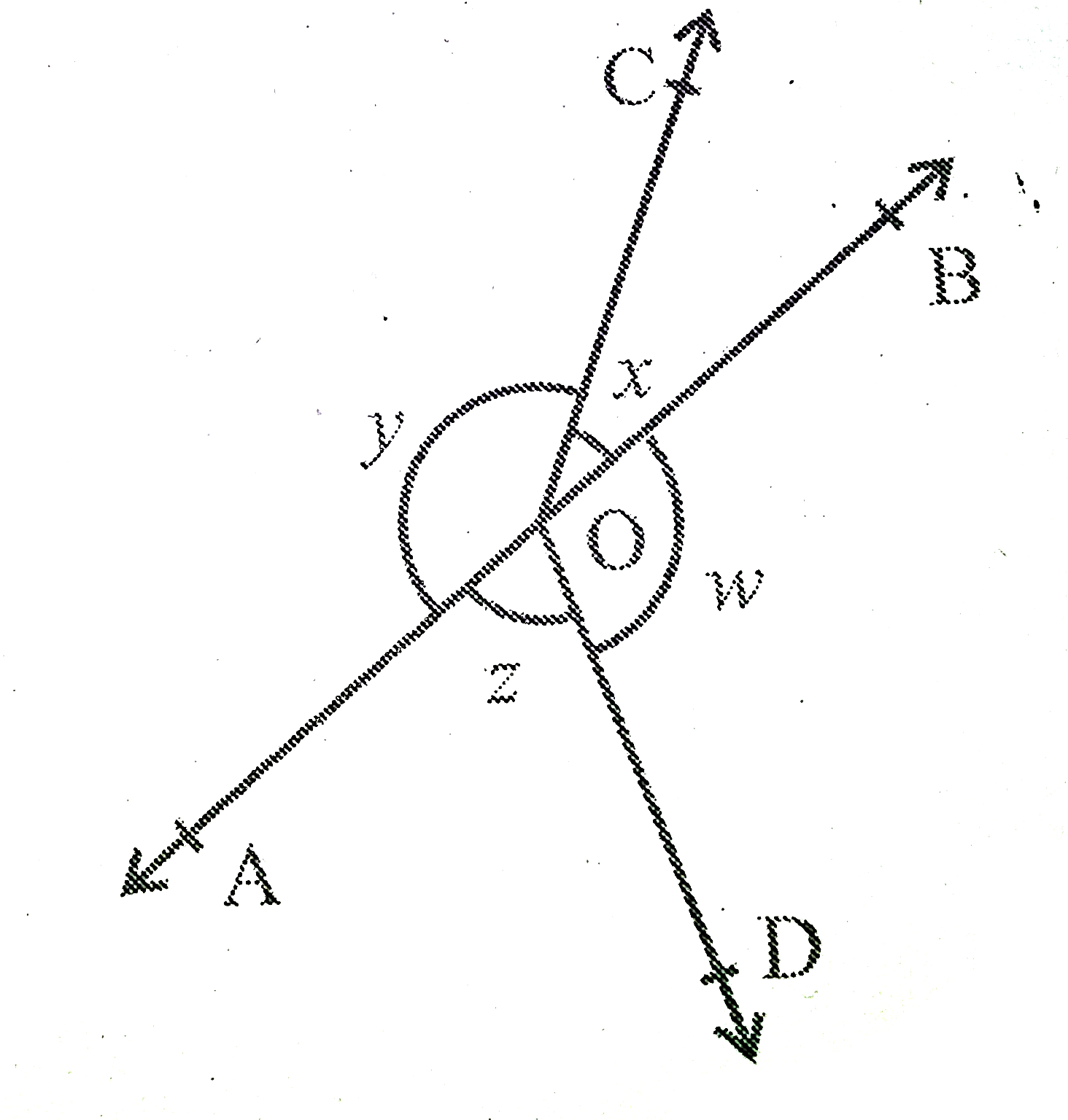
View SolutionIn the given figure, if x+y=z+w then prove that AOB is a line.
View SolutionIn Fig. 4.97, if ∠A=∠C , then prove that AOB~COD . (FIGURE)
View SolutionA line perpendicular to the axis of the parabola y2=16x intersects the parabola in two points A and B . If AB = 32 , show that ∠AOB is a right angle . Also , find the area of ΔAOB .
View SolutionIn Fig. 6.46, if y is five times x, find the value of z.
View SolutionIn Fig. 6.40, find the values of x, y and z.

View SolutionIf the 4th, 10th and 16th terms of a GP are x, y, z respectively, prove that x, y, z are in GP.
View SolutionIf the 4th, 10th and 16 th terms of a G.P. are x, y and z, respectively. Prove that x,y,z are G.P.
View SolutionIf ω is non-real cube roots of unity, then prove that ∣∣∣x+yω+zω2xw+z+yω2∣∣∣=1
View Solution

