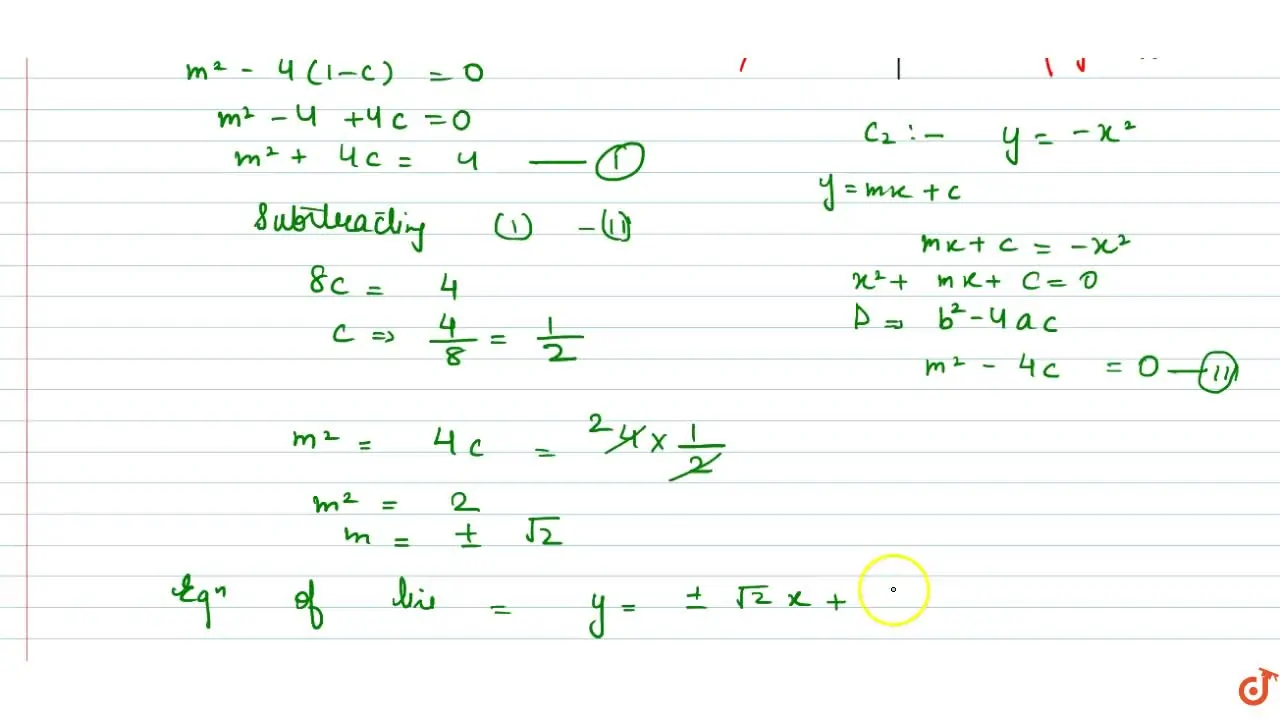Equation of a line which is tangent to both the curve y=x2+1 and y=x2 is y=√2x+12 (b) y=√2x−12 y=−√2x+12 (d) y=−√2x−12
Step by step video & image solution for Equation of a line which is tangent to both the curve y=x^2+1\ a n d\ y=x^2 is y=sqrt(2)x+1/2 (b) y=sqrt(2)x-1/2 y=-sqrt(2)x+1/2 (d) y=-sqrt(2)x-1/2 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
Equation of a line which is tangent to both the curve y=x2+1 and y=x2 is y=√2x+12 (b) y=√2x−12 y=−√2x+12 (d) y=−√2x−12
View SolutionFind the equation of tangent to the curve y=sin−1(2x)1+x2atx=√3
View SolutionThe equation of tangent to the curve y=∫x3x2dt√1+t2 at x=1 is √3x+1=y (b) √2y+1=x √3x+y=1 (d) √2y=x
View SolutionThe area bounded by the curves y=|x|−1andy=−|x|+1 is a.1 b. 2 c. 2√2 d. 4
View SolutionThe radius of a circle, having minimum area, which touches the curve y=4−x2 and the lines, y=|x| is: (a) 4(√2+1) (b) 2(√2+1) (c) 2(√2−1) (d) 4(√2−1)
View SolutionIf the line ax + y = c, touchs both the curves x2+y2=1
and y2=4√2x, then |c| is equal toView SolutionArea of the region enclosed between the curves x=y2−1 and x=|y|√1−y2 is
View SolutionAea of the region nclosed between the curves x=y2−1 and x=|y|√1−y2 is
View SolutionIf the line ax+y=c, touches both the curves x2+y2=1andy2=4√2x, then |c| is equal to:
View SolutionA beam of light is sent along the line x−y=1 , which after refracting from the x-axis enters the opposite side by turning through 300 towards the normal at the point of incidence on the x-axis. Then the equation of the refracted ray is (a) (2−√3)x−y=2+√3 (b) (2+√3)x−y=2+√3 (c) (2−√3)x+y=(2+√3) (d) y=(2−√3)(x−1)
View Solution