The steady state current in a 2Ω resistor when the internal resistance of the battery is negligible and the capacitance of the condenser is 0.1μF is
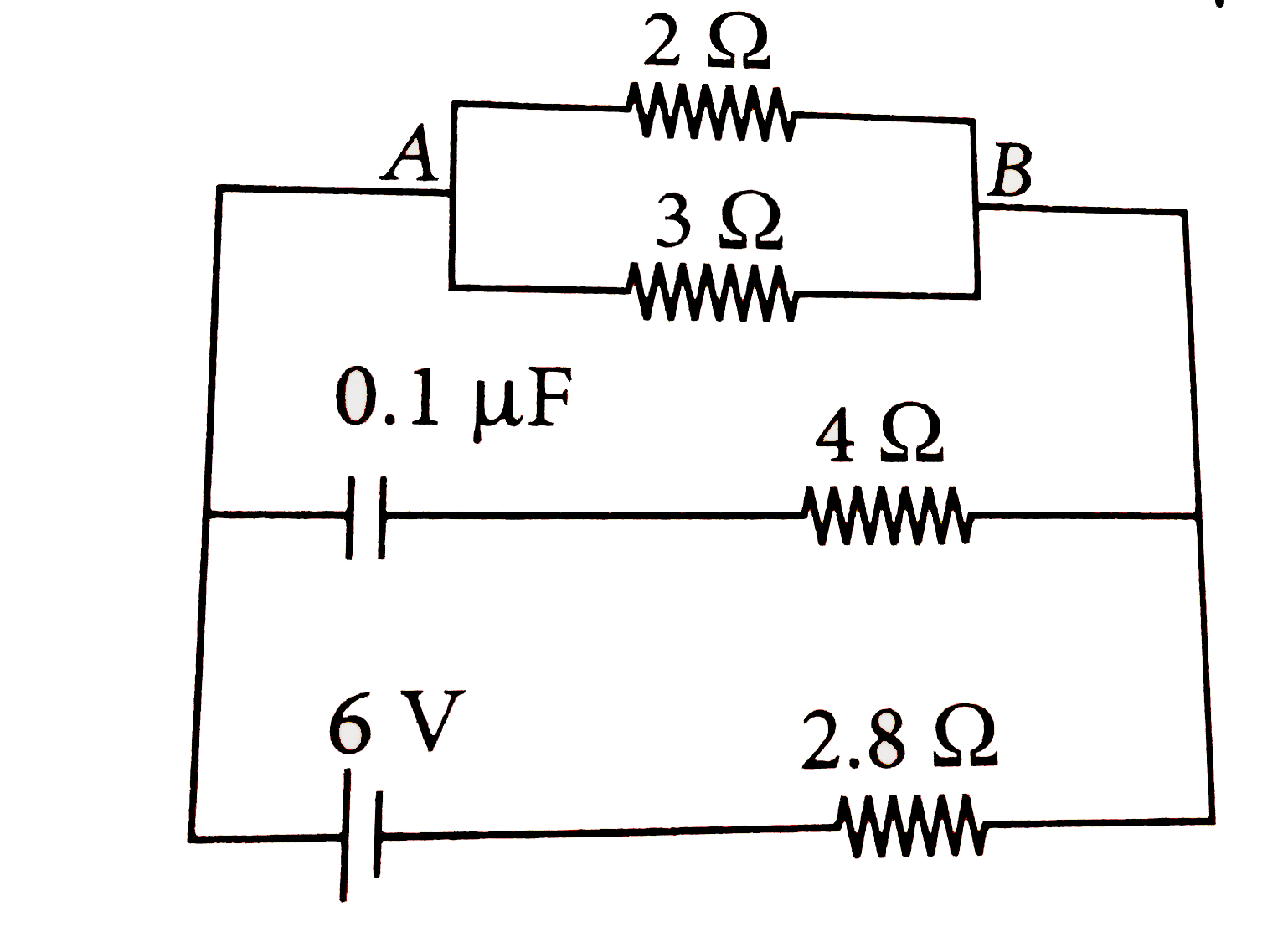
0.6A
0.9A
1.5A
0.3A
The correct Answer is:B
Step by step video, text & image solution for The steady state current in a 2 Omega resistor when the internal resistance of the battery is negligible and the capacitance of the condenser is 0.1 mu F is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PRACTICE PAPPERBOOK - NCERT FINGERTIPSCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 2
50 Videos
- PRACTICE PAPPERBOOK - NCERT FINGERTIPSCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 3
50 Videos
- NUCLEIBOOK - NCERT FINGERTIPSCHAPTER - NUCLEIEXERCISE - Assertion And Reason
15 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTIPSCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
Calculate the steady state current in the 2- ohm resistor shown in the circuit in the figure. The intermal resistance of the battery is negligible and the capacitance of the condenser C is 0.2 microfarad.
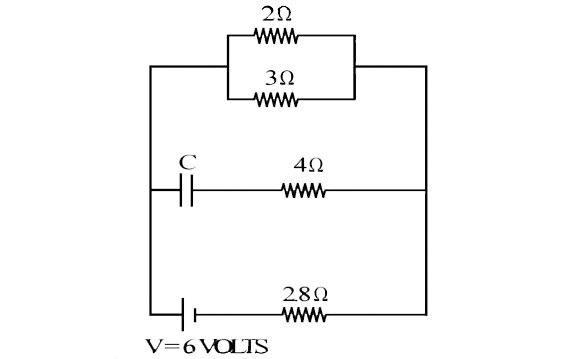
View SolutionCalculate the steady state current (in A ) in the 2μ resistor shown in the circuit (see figure). The internal resistance of the battery is negligible and the capacitance of the condenser C is 0.2μF

View Solution
Knowledge Check
Calculate the steady state current in the 2Ω resistor, shown in figure. The internal resistance of the battery is negligible and the capacitance of the capacitor C is 0.2μF.
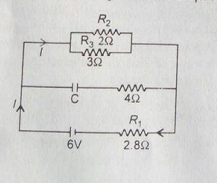 A1.0AB0.9AC1.2AD0.8A
A1.0AB0.9AC1.2AD0.8ACalculate the steady state current in the 2Ω resistor, shown in figure. The internal resistance of the battery is negligible and the capacitance of the capacitor C is 0.2μF.
 A1.0AB0.9AC1.2AD0.8A
A1.0AB0.9AC1.2AD0.8AIn fig the steady state current in 2ω resistance is
 A0.3AB0.9AC0.6ADzero
A0.3AB0.9AC0.6ADzero
Calculate the steady-state current through 2Ω resistor in the circuit shown in Fig. 4.42. The internal resistance of the battery is negligible and C=2μF.
View SolutionAn inductor of inductance L=400 mH and resistor of resistance R1=2(Ω)andR2=2(Ω) are connected to a battery of emf E = 12 Vas shown in the figure. The internal resistance of the battery is negligible. The switch S is closed at time t =0. What is the potential drop across L as a function of time? After the steady state is reached, the switch is opened. What is the direction and the magnitude of current through R1 as a function of time?
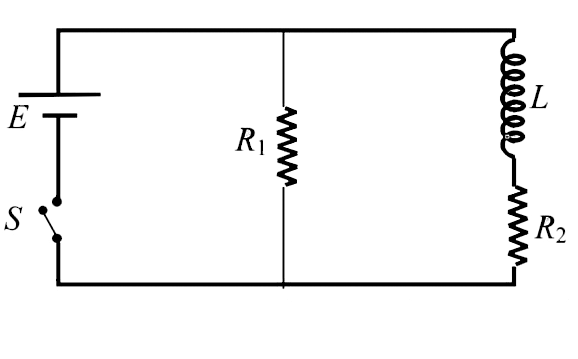
View SolutionAn inductor of inductance L=400mH and resistors of resistances R1=2Ω and R2=2Ω are connected to a battery of emf E=12V as shown in the figure. The internal resistance of the battery is negligible. The switch S is closed at time t=0.

What is the potential dro across L s a function of time? After the steady state is reached, the switch is opened. What is the direction ad the magnitude of current throough R1 as a function of time?
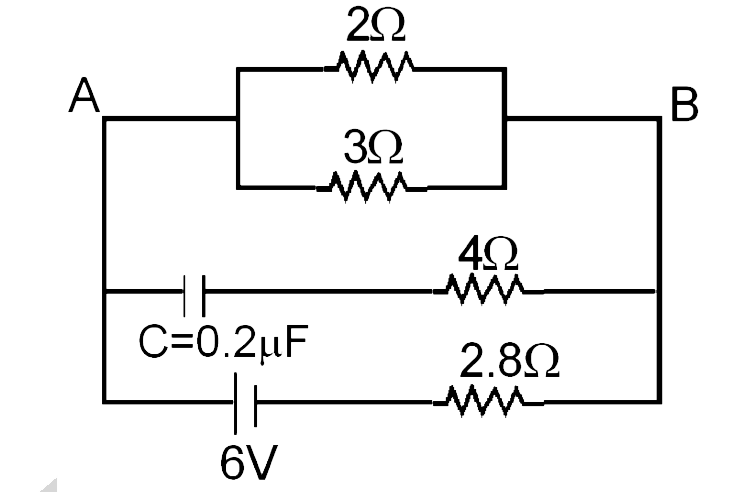
View SolutionTaking the internal resistance of the battery as negligible, the steady state current in the 2ohm resistor shown in the figure will be

View SolutionTaking the internal resistance of the battery as negligible, the steady state current in the 2ohm resistor shown in the figure will be

View Solution
