What is the minimum thickness of a soap bubble needed for constructive interference in reflected light, if the light incident on the film is 750 nm? Assume that the refractive index for the film is n=1.33
282 nm
70.5 nm
141 nm
387 nm
The correct Answer is:C
As, 2μtmin=λ2
∴tmin=λ4μ=7504×1.33=141nm
Topper's Solved these Questions
- WAVE OPTICSBook:NCERT FINGERTIPSChapter:WAVE OPTICSExercise:Diffraction
Explore 22 Videos
- WAVE OPTICSBook:NCERT FINGERTIPSChapter:WAVE OPTICSExercise:Polarisation
Explore 18 Videos
- WAVE OPTICSBook:NCERT FINGERTIPSChapter:WAVE OPTICSExercise:Coherent And Incoherent Addition Of Waves
Explore 7 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS Book:NCERT FINGERTIPSChapter:SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS Exercise:Assertion And Reason
Explore 15 Videos
Similar Questions
If the wavelength of incident light on a soap film is 700 nm then its minimum thickness 10 t nm so that constructive interference in reflected light can be observed. The value of t is ………..[Take refractive index of the film as 43]
View SolutionCalculate the minimum thickness of a soap bubble film (μ=1.33)that results in constructive interference in the reflected light if the film is illuminated with light whose wavelength in free space is λ=600nm.
View Solution
Knowledge Check
What is the minimum thickness of thin film required for constructive interference in the reflected light through it ?
(Given, the refractive index of the film =1.5, wavelength of the lilght incident on the film =600 nm.A100nmB150nmC200nmD250nmWhat is the minimum thickness of thin film required for constructive interference in the reflected light through it ?
(Given, the refractive index of the film =1.5, wavelength of the lilght incident on the film =600 nm.A100 nmB50 nmC200 nmD25 nmWhat is the minimum thickness of a thin film (μ=1.2) that results in constructive interference in the reflected light? If the film is illuminated with light whose wavelength in free space is λ=500nm ?
A104 nmB200 nmC300 nmD400 nm
An oil film covers the surface of a small pond. The refractive index of the oil is greater than that of water. At one point on the film, the film has the smallest non-zero thickness for which there will be destructive interference in the reflected light when infrared radiation with wavelength 800 nm is incident normal to the film. When this film is viewed at normal incidence at this same point, for what visible wavelengths, if any, will there be constructive interference? (Visible light has wavelengths between 400nm and 700 nm )
View SolutionRefractive index of a thin soap film of a uniform thickness is 1.38. The smallest thickness of the film that gives an interference maxima in the reflected light when light of wavelength 5520 Å falls at normal incidence is
View SolutionFor observing interference in thin films with a light of wave length λ the thickness of the film:
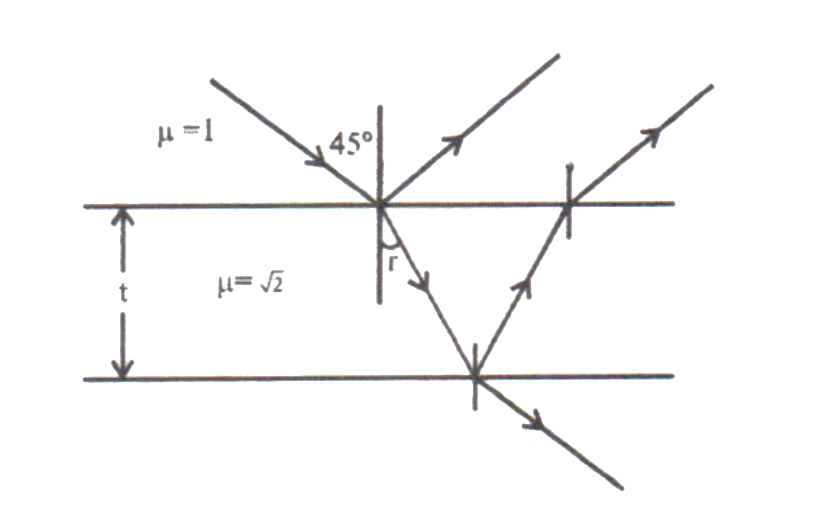
View SolutionA ray of light is incident at an angle of 45∘ (ralative to the normal) on a thin film of a liquid with an index of refraction of √2. Assuming that the medium of both sides of the film is air, find the minimum thickness of the film required for constructive interference in the reflected light for sodium light of wavelenght 600 nm.
View SolutionA thin uniform film of refractive index 1.75 is placed on a sheet of glass of refractive index 1.5. At room temperature (20∘C) this film is just thick enoungh for light with wavelength 600 nm reflected off the top of the film to be canceled by light reflected from the top the glass. After the glass is placed in on oven and slowly heated to 170∘C, the film conceals reflected light with wavelength 606 nm. The coefficient of linear expansion of the film is (ignore any changes in the refractive index of the film due to the temperature change)
View Solution

