When a current of 2 A flows in a battery from negative to positive terminal, the potential difference across it is 12 V. If a current of 3 A flowing in the opposite direction produces a potential difference of 15 V, the emf of the battery is
12.6V
13.2V
13.5V
14.0V
The correct Answer is:B
To find the EMF of the battery, we will analyze the two cases provided in the question step by step.
Step 1: Analyze Case 1
In the first case, a current of 2 A flows from the negative to the positive terminal, resulting in a potential difference of 12 V across the battery.
- Let e be the EMF of the battery.
- Let r be the internal resistance of the battery.
Using Ohm's law, the potential difference across the internal resistance can be expressed as:
V=I⋅r
For a current of 2 A:
V=2r
Applying Kirchhoff's loop rule, we can write:
e−2r−12=0
Rearranging gives us:
e=12+2r(Equation 1)
Step 2: Analyze Case 2
In the second case, a current of 3 A flows in the opposite direction, resulting in a potential difference of 15 V across the battery.
Using Ohm's law again, for a current of 3 A:
V=3r
Applying Kirchhoff's loop rule for this case gives us:
e−3r+15=0
Rearranging gives us:
e=15+3r(Equation 2)
Step 3: Equate the Two Equations
Now we have two equations for e:
1. e=12+2r
2. e=15+3r
Setting these two equations equal to each other:
12+2r=15+3r
Step 4: Solve for r
Rearranging the equation:
12−15=3r−2r
−3=r
Thus, we find:
r=3ohms
Step 5: Substitute r Back to Find e
Now, substitute r back into either Equation 1 or Equation 2 to find e. Using Equation 1:
e=12+2(3)
e=12+6=18V
Final Answer
The EMF of the battery is 18 V.
---
In the first case, a current of 2 A flows from the negative to the positive terminal, resulting in a potential difference of 12 V across the battery.
- Let r be the internal resistance of the battery.
V=I⋅r
For a current of 2 A:
V=2r
e−2r−12=0
Rearranging gives us:
e=12+2r(Equation 1)
In the second case, a current of 3 A flows in the opposite direction, resulting in a potential difference of 15 V across the battery.
V=3r
e−3r+15=0
Rearranging gives us:
e=15+3r(Equation 2)
Now we have two equations for e:
1. e=12+2r
2. e=15+3r
12+2r=15+3r
Rearranging the equation:
12−15=3r−2r
−3=r
Thus, we find:
r=3ohms
Now, substitute r back into either Equation 1 or Equation 2 to find e. Using Equation 1:
e=12+2(3)
e=12+6=18V
The EMF of the battery is 18 V.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:NCERT FINGERTIPSChapter:CURRENT ELECTRICITYExercise:Cell In Series And In Parallel
Explore 3 Videos
- CURRENT ELECTRICITYBook:NCERT FINGERTIPSChapter:CURRENT ELECTRICITYExercise:Kirchoff'S Law
Explore 11 Videos
- CURRENT ELECTRICITYBook:NCERT FINGERTIPSChapter:CURRENT ELECTRICITYExercise:Combination Of Resistors : Series And Parallel
Explore 22 Videos
- COMMUNITCATION SYSTEMSBook:NCERT FINGERTIPSChapter:COMMUNITCATION SYSTEMSExercise:HOTS
Explore 10 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:NCERT FINGERTIPSChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:Assertion And Reason
Explore 15 Videos
Similar Questions
The potential difference across terminals of a battry is 9.0V, when a current of 3.5A flows through it from its negative terminal to the positive terminal .When a current of 2A flows through in the opposite direction, the terminal potential difference is 12V. Find the internal resistance and emf of the battery
View SolutionThe potential difference across the terminals of a battery is 8.4V when there is a current of 1.50A in the battery from the negative to the positive terminal. When the current is 3.50Air, the reverse direction, the potential difference becomes 9.4V.
(a) What is the internal resistance of the battery?
(b) What is the emf of the battery?
View Solution
Knowledge Check
When a current of 2 A flows in a battery from negative to positive terminal, the potential difference across it is 20 V. If a current of 3 A flowing in the opposite direction produces a potential difference of 25 V, the emf of the battery is
A20 VB22 VC15.5 VD14 VPotential difference across the terminal of a non ideal battery is
Azero when it is short circuitedBless than its emf when current flows from negative terminal to positive terinal inside the batteryCzero when no current is drawn from the batteryDgreater than its emf when current flows from positive terminal to negative terminal inside the batteryThe potential difference across te terminals of a battery is 10 V when there is a current of 3 A in the battery from the negative to the positive terminal. When the current is 2A in the reverse direction, the potential difference becomes 15 V. The internal resistance of the battery is
A1ΩB0.4ΩC0.6ΩD0.8Ω
Can the potential difference across a battery be greater than its emf?
View SolutionState the condition under which the terminal potential difference across a battery and its emf are equal.
View SolutionWhen a current drawn from a battery is 0.5 A, its terminal potential difference is 20 V. And when current drawn from it is 0.2 A, the terminal voltage reduces to 16 V. Find out, emf and internal resistance of the battery.
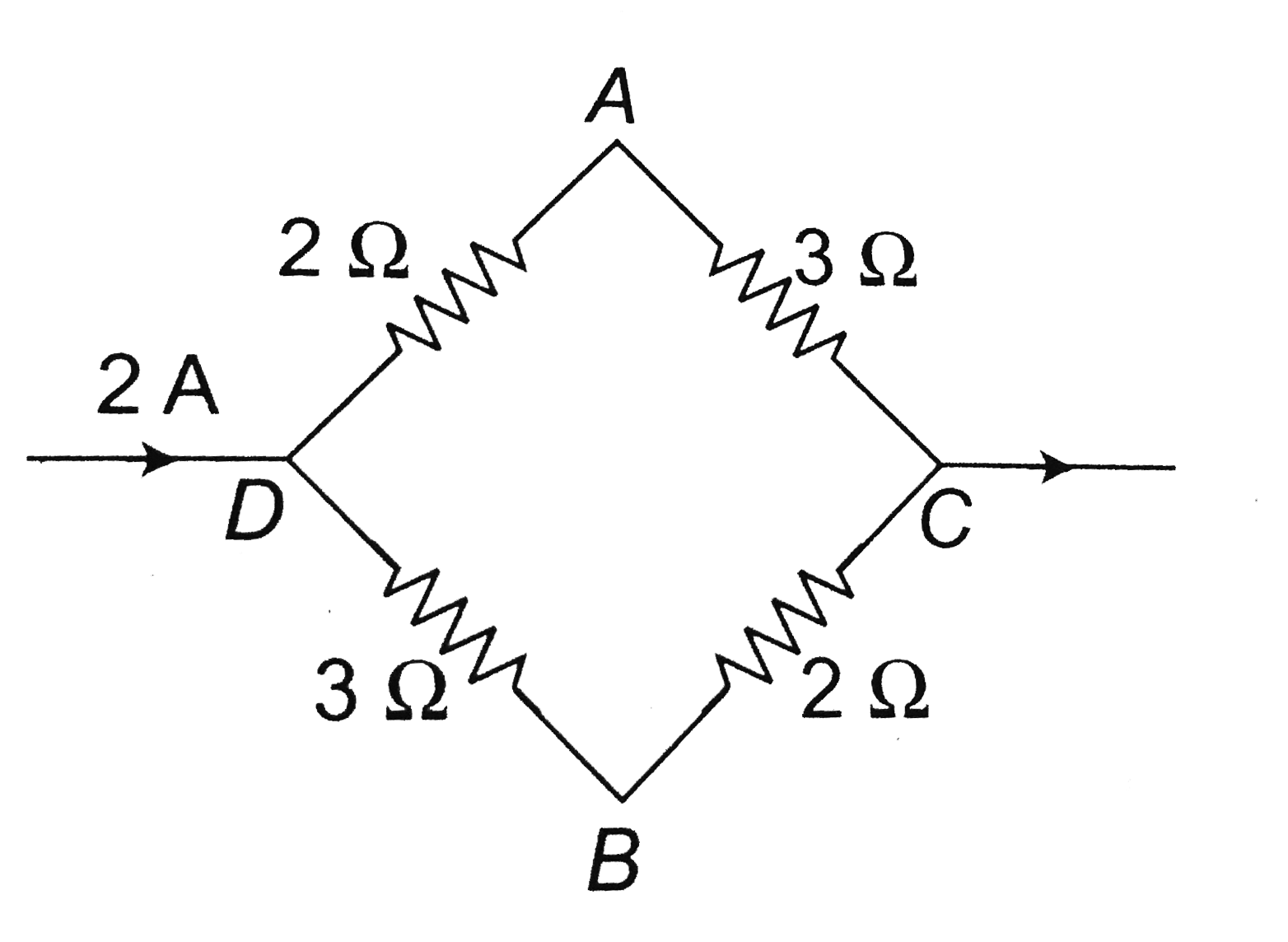
View SolutionA current of 2A flows in a system of conductor as shown. The potential difference (VA−VB)
View SolutionIf the potential difference across the ends of a conductor is doubled, the current flowing through it gets
View Solution

