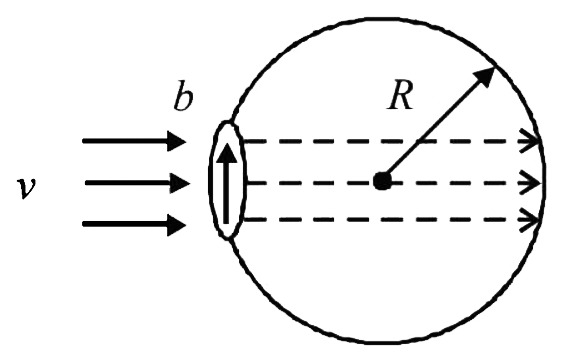
A bubble having surface tension T and radius R is formed on a ring of radius b(b<<R). Air is blown inside the tube with velocity v as shown. The air molecule collides perpendicularly with the wall of the bubble and stops. Calculate the radius at which the bubble separates from the ring.
2Tρv2
2Tρv
4Tρv2
4Tρv
The correct Answer is:C
Excess pressure inside a bubble =4TR
Let area of bubble at wall where air strikes be A.
∴ Force due to excess pressure=4TAR
Let ρ=density of air, Force due to striking air=ρAv2
For bubble to separate from the ring,
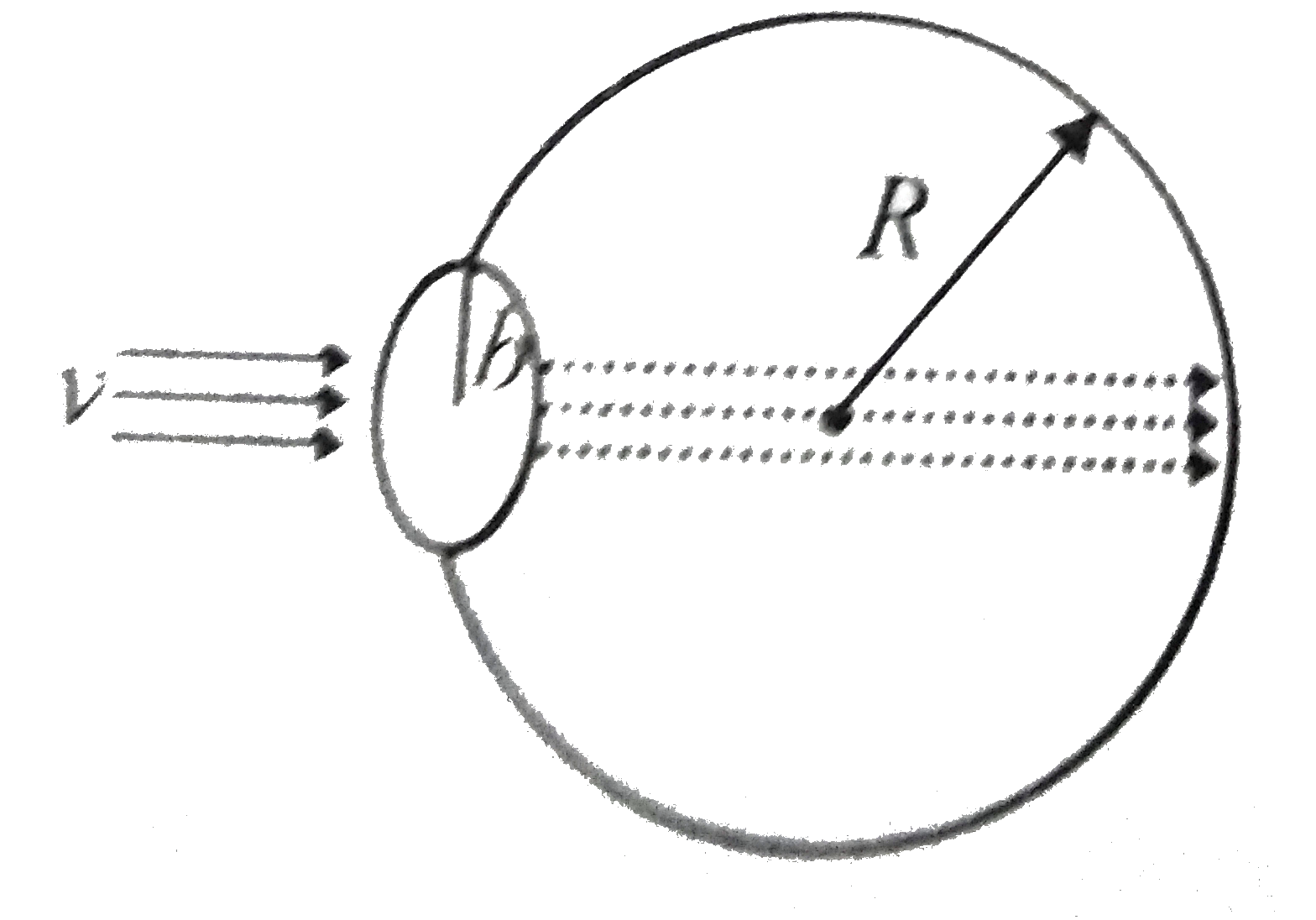
ρAv2 or ρAv2R=4TA or R=4Tρv2
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBook:NCERT FINGERTIPSChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:NCERT Exemplar
Explore 5 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NCERT FINGERTIPSChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Assertion And Reason
Explore 15 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NCERT FINGERTIPSChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Surface Tension
Explore 31 Videos
- LAWS OF MOTIONBook:NCERT FINGERTIPSChapter:LAWS OF MOTIONExercise:Assertion And Reason
Explore 15 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NCERT FINGERTIPSChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:Assertion And Reason
Explore 15 Videos
Similar Questions
A bubble having surface tension T and radius R is formed on a ring of radius b (b<>R) . Air is blown inside the tube held in front of the ring , with velocity υ as shown in fig. The air molecules collides perpendicularly with the wall of the bubble and stops. Calculate the radius R at which the bubble and stops. Calculate the radius R at which the bubble separates from the ring.
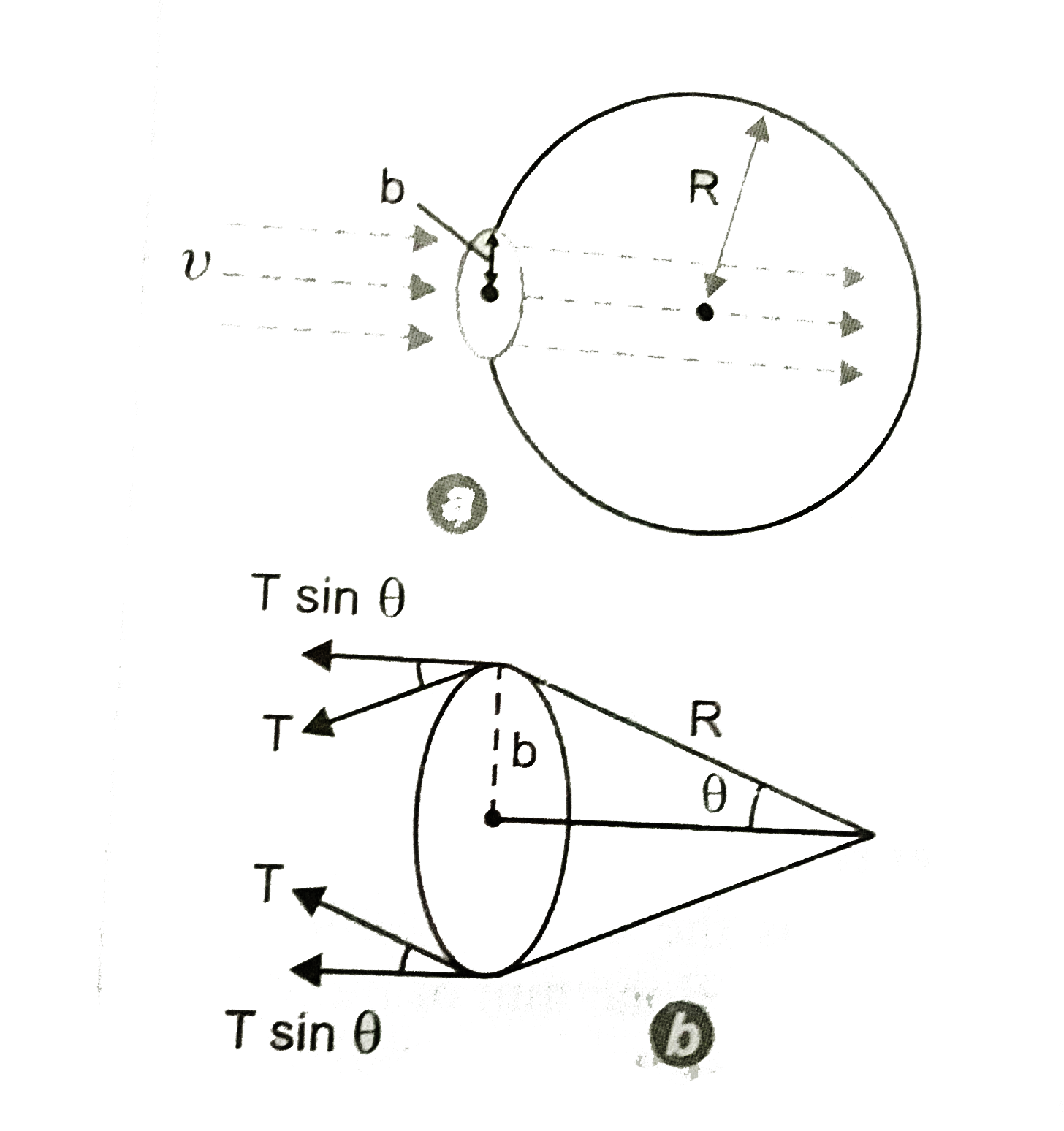
View SolutionA bubble having surface tension T and radius R is formed on a ring of radius b (b<>R) . Air is blown inside the tube held in front of the ring , with velocity υ as shown in fig. The air molecules collides perpendicularly with the wall of the bubble and stops. Calculate the radius R at which the bubble and stops. Calculate the radius R at which the bubble separates from the ring.

View Solution
Knowledge Check
The surface tension of soap is T . The work done in blowing a soap bubble of radius 3 R to that of a radius 5R is
A64πR2TB100πR2TC128πR2TD256πR2TIf R is the radius of a soap bubble and S its surface tension, then the excess pressure inside is
A2SRB3SRC4SRDSRA charged soap bobbe having surface charge density σ and radius r. If the pressure inside and outsides the soap bubble is the same, then the surface tension of the soap solution is
AT=σ2R8ε0BT=σ2R4ε0CT=σ2R2ε0DT=σ2Rε0
Two air bubbles with radius r are present in water. Are these bubbles attracted or repelled?
View SolutionThere is a soap bubble of radius 2.4×10−4m in air cylinder at a pressure of 105N/m2. The air in the cylinder is compressed isothermal untill the radius of the bubble is halved. Calculate teh new pressure of air in the cylinder. Surface tension of soap solution is 0.08Nm−1.
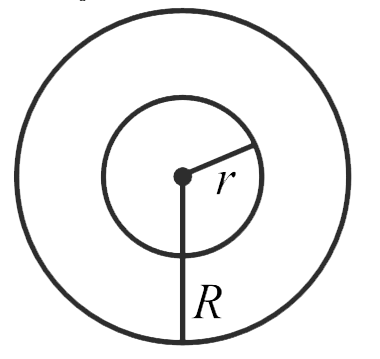
View SolutionA soap bubble of radius r is formed inside another soap bubble of radius R(>r). The atmospheric pressure is P0 and surface tension of the soap solution is T. Calculate change in radius of the smaller bubble if the outer bubble bursts. Assume that the excess pressure inside a bubble is small compared to P0.
View SolutionIf a small air bubble of radius 0.1 mm is formed just below the surface of water, then the pressure inside the air bubble will be
View SolutionAir is pushed in a soap bubble to increase its radius from R to 2R . In this case the pressure inside the bubble
View Solution

