If stress-strain relation for volametric change is in the from ΔVV0=KP where P is applied uniform pressure, then K stands for
shear modulus
compressibility
Young's modulus
bulk modulus
The correct Answer is:B
Bulk modulus =PΔV/V
Compressibility = 1Bulk modulus=ΔV/VP=K(Compressibility)
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBook:NCERT FINGERTIPSChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:Applications Of Elastic Behaviour Of Materials
Explore 8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NCERT FINGERTIPSChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:Higher Order Thinking Skills
Explore 8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NCERT FINGERTIPSChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:Stress-Strain Curve
Explore 5 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NCERT FINGERTIPSChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Assertion And Reason
Explore 15 Videos
- MOTION IN A PLANE Book:NCERT FINGERTIPSChapter:MOTION IN A PLANE Exercise:Assertion And Reason
Explore 15 Videos
Similar Questions
An ideal gas (CpCv=γ)has initial volume V0 is kept in a vessel. It undergoes a change and follows the following relation P=kV2 (where P is pressure, and V is volume) find the change in internal energy of the gas if its final pressure is P0:
View SolutionTwo soap bubble are combined isothermally to form a big bubble of radius R. If ΔV is change in volume, ΔS is change in surface area and P0 is atmospheric pressure then show that 3P0(ΔV)+4T(ΔS)=0
View Solution
Knowledge Check
For a constant hydraulic stress on an object, the fractional change in the object's volume (△VV) and its bulk modulus (b) are related as
AΔVV∝KBΔVV∝1KCΔVV∝K2DΔVV∝K−2The dimensions of γ in the relation v=√γpρ (where v is velocity, p is pressure , ρ is density)
ADimensionlessB[LT−1]C[ML−1T−2]D[ML−3]For a constant hydraulic pressure on an object, the fractional change in the object's volume (ΔVV) and its compressibility (1K) are related as
AΔVV∝KBΔVV∝K2CΔVV∝1KDΔVV∝1K2
A sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P2.
Which relation is correct (γ=CPCV)?
View SolutionThe compressibility of a material is B.A cube of side 'a' is made with this material. If a uniform pressure P is applied on the cube from all the sides the fractional change in its length will be
View SolutionPressure P, Volume V and temperature T of a certain material are related by the P=αT2V. Here α is constant. Work done by the material when temparature changes from T0 to 2T0 while pressure remains constant is :
View SolutionThe work done in changing the state from (P0,V0) to (P1,V1) in the following system is :
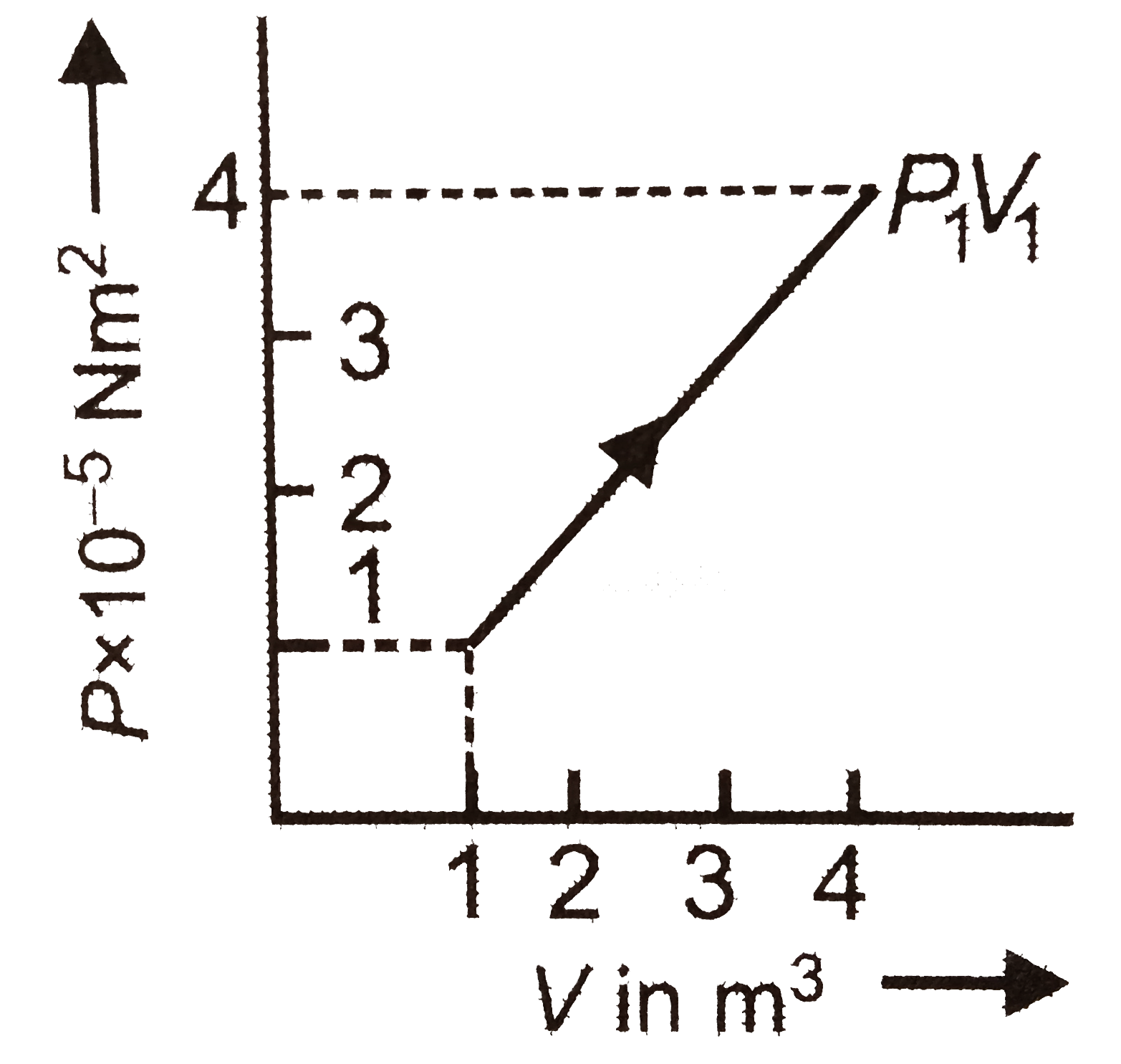
View SolutionAt constant temperature, the equilibrium constant (Kp) for the decomposition reaction N2O4⇔2NO2 is expressed Kp=4x2P(1−x2), where P= pressure, × =extent of decomposition. Which one of the following statements is true?
View Solution

