A particle in a certain conservative force field has a potential energy given by . The force exerted on it is
The correct Answer is:B
Given :
For a conservative field
Topper's Solved these Questions
- WORK , ENERGY AND POWERBook:NCERT FINGERTIPSChapter:WORK , ENERGY AND POWERExercise:The Conservation Of Mechanical Energy
Explore 12 Videos
- WORK , ENERGY AND POWERBook:NCERT FINGERTIPSChapter:WORK , ENERGY AND POWERExercise:The Potential Energy Of A Spring
Explore 6 Videos
- WORK , ENERGY AND POWERBook:NCERT FINGERTIPSChapter:WORK , ENERGY AND POWERExercise:The Work Energy Theorem For A Variable Force
Explore 3 Videos
- WAVESBook:NCERT FINGERTIPSChapter:WAVESExercise:Assertion And Reason
Explore 15 Videos
Similar Questions
Knowledge Check
A particle in a certain conservative force field has a potential energy given by U=20xyz. The force exerted on it is
A(20yz)ˆi+(20xz)ˆj+(20xyz2)ˆkB−(20yz)ˆi−(20xz)ˆj+(20xyz2)ˆkC−(20yz)ˆi−(20xz)ˆj−(20xyz2)ˆkD(20yz)ˆi+(20xz)ˆj−(20xyz2)ˆkThe relation between conservative force and potential energy U is given by :–
A→F=dUdxB→F=∫UdxC→F=−dUdxD→F=d2Udx2In a conservative field at stable equilibrium potential energy is:
AmaximumBminimumCconstantDmaximum or minimum
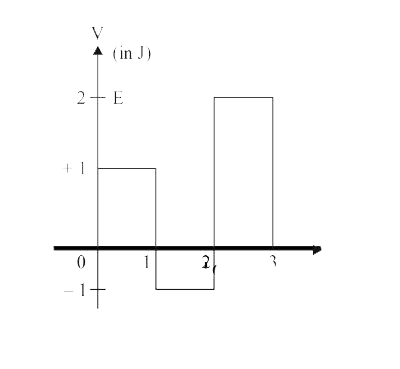
A particle moves in one dimension in a conservation force field. The potential energy is depicted in the graph below.
If the particle starts to move from rest from the point A, then
View SolutionAssertion: Frictional force are conservative forces.
Reason: Potential energy change can be assorciated with frictional forces.
View SolutionA particle of mass m=3 kg is moving on a straight line in a conservative force field in which the potential energy associated with the particle is given by U(y)=2y2−30y+450. At t=0, particle is at y=8m and moving towards positive y- axis with 1m/s
View SolutionA particle is moving in a conservative force field from point A to point B.UA and UB are the potential energies of the particle at point A and B and WC is the work done by conservative forces in the process of taking the particle from A and B, which of the following is true?
View SolutionA particle is executing simple harmonic motion in a conservative force field. The total energy of simple harmonic motion is given by E=ax2+bv2where ‘x’ is the displacement from mean position x = 0 and v is the velocity of the particle at x then choose the INCORRECT statements.{Potential energy at mean position is assumed to be zero}
View Solution