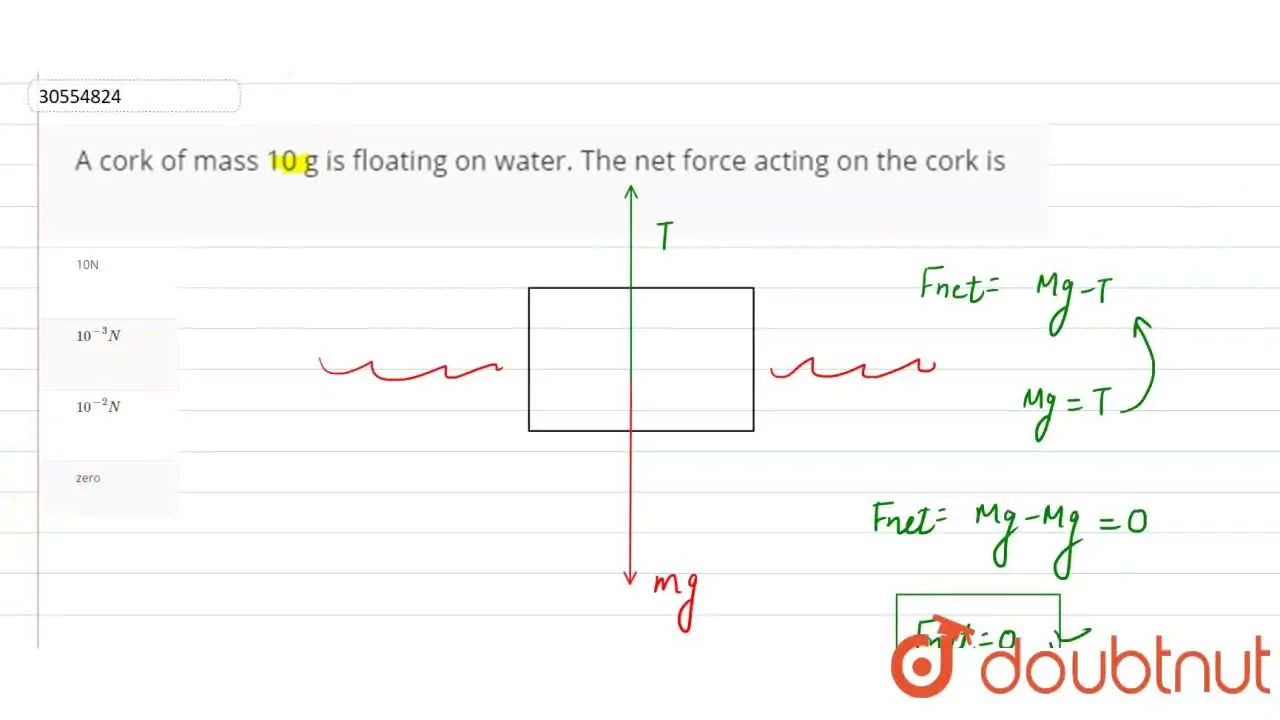
A cork of mass 10 g is floating on water. The net force acting on the cork is
10N
10−3N
10−2N
zero
The correct Answer is:D
When the cork is floating its weight is balanced by the upthrust. Therefore net force on the cork is zero.
Related Playlists
- BOOK - NCERT FINGERTIPSCHAPTER - LAWS OF MOTIONEXERCISE - Conservation Of Momentum4videos
LAWS OF MOTION
- BOOK - NCERT FINGERTIPSCHAPTER - LAWS OF MOTIONEXERCISE - Equilibrium Of A Particle6videos
LAWS OF MOTION
- BOOK - NCERT FINGERTIPSCHAPTER - LAWS OF MOTIONEXERCISE - Newton'S Second Law Of Motion19videos
LAWS OF MOTION
- BOOK - NCERT FINGERTIPSCHAPTER - KINETIC THEORYEXERCISE - Assertion And Reason10videos
KINETIC THEORY
- BOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Assertion And Reason15videos
MECHANICAL PROPERTIES OF FLUIDS
Similar Questions
A cork of mass 10g is floating on water. The net force acting on the cork is
View SolutionA piece of cork isfloating on water. What is the net force acting on it ?
View SolutionThe net force acting is not zero on
View SolutionA stone of mass l kg is lying on the floor of a train which is accelerating with 1ms−2 The net force acting on the stone is
View SolutionA cork is floating in a water tube. What is the apparent weight of the cork ?
View SolutionIf the displacement x of a particle of mass m is directly proportionalto time, net force acting on it is ________________.
View SolutionA razor blade can be made to float on water. What force act on this blade? Is Archimedes principle applicable?
View SolutionA place of cork is floating on water in a small tank. The cork oscillates up and down vertically when small ripples pass over the surface of water. The velocity of the ripples being 0.21ms−1, wave length 15mm, and amplitude 5mm, the maximum velocity of the piece of cork is (π=227)
 View Solution
View SolutionA body of mass 10 kg is acted upon by a net force F which varies with time t as shown in figure. Then the net momentum in SI units gained by the body at the end of 10 seconds is
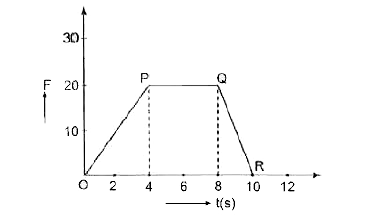 View Solution
View SolutionThe vessel shown in the figure contains water, take ρwater=1000kg/m2,g=m/s2). For this arrangement, answer the following questions:
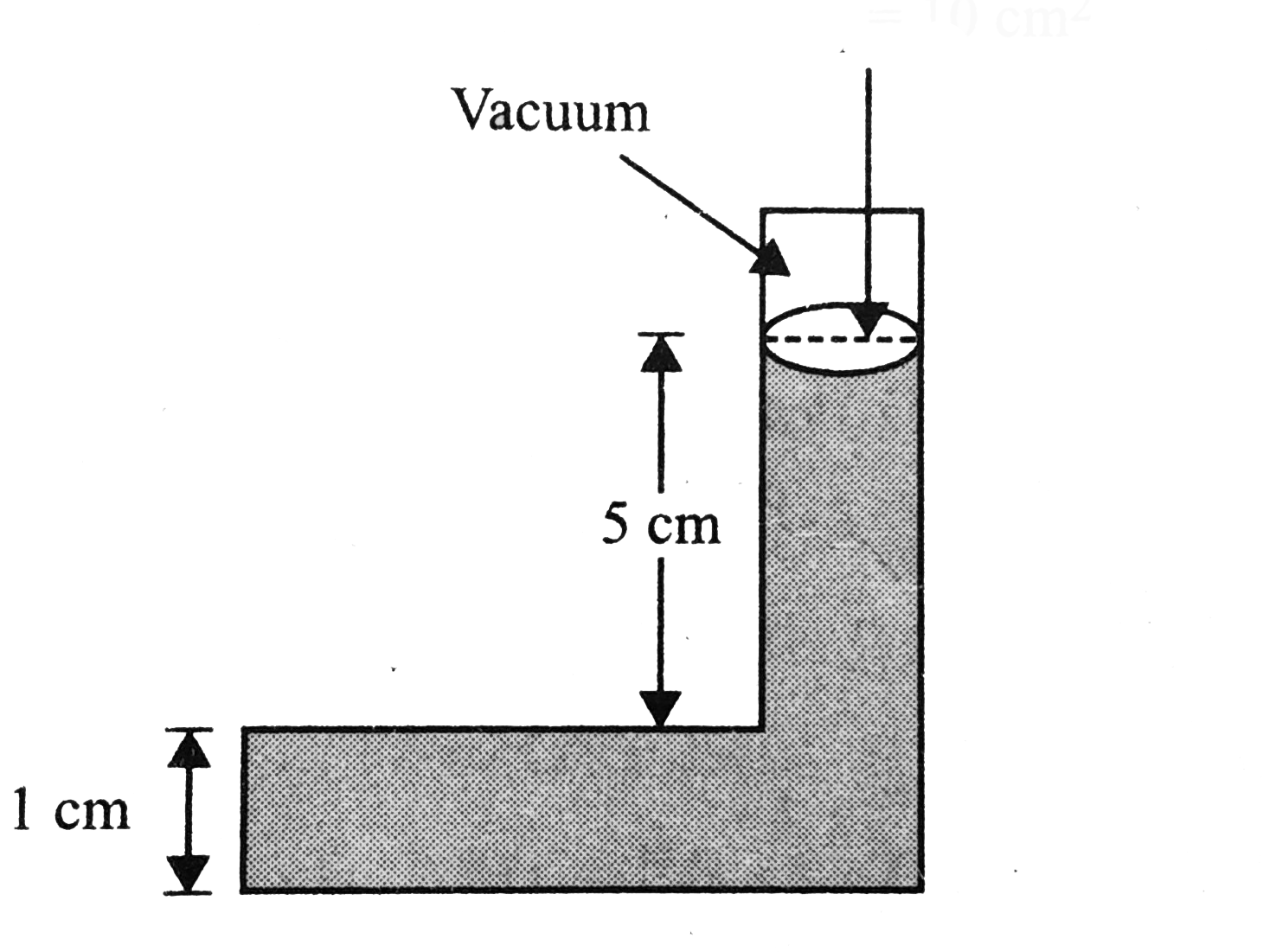
The net force acting on the base of the vessel isView Solution