One mole of a monoatomic real gas satisfies the equation p(V−b)=RT where b is a constant. The relationship of interatomic potential V(r) and interatomic distance r for gas is given by
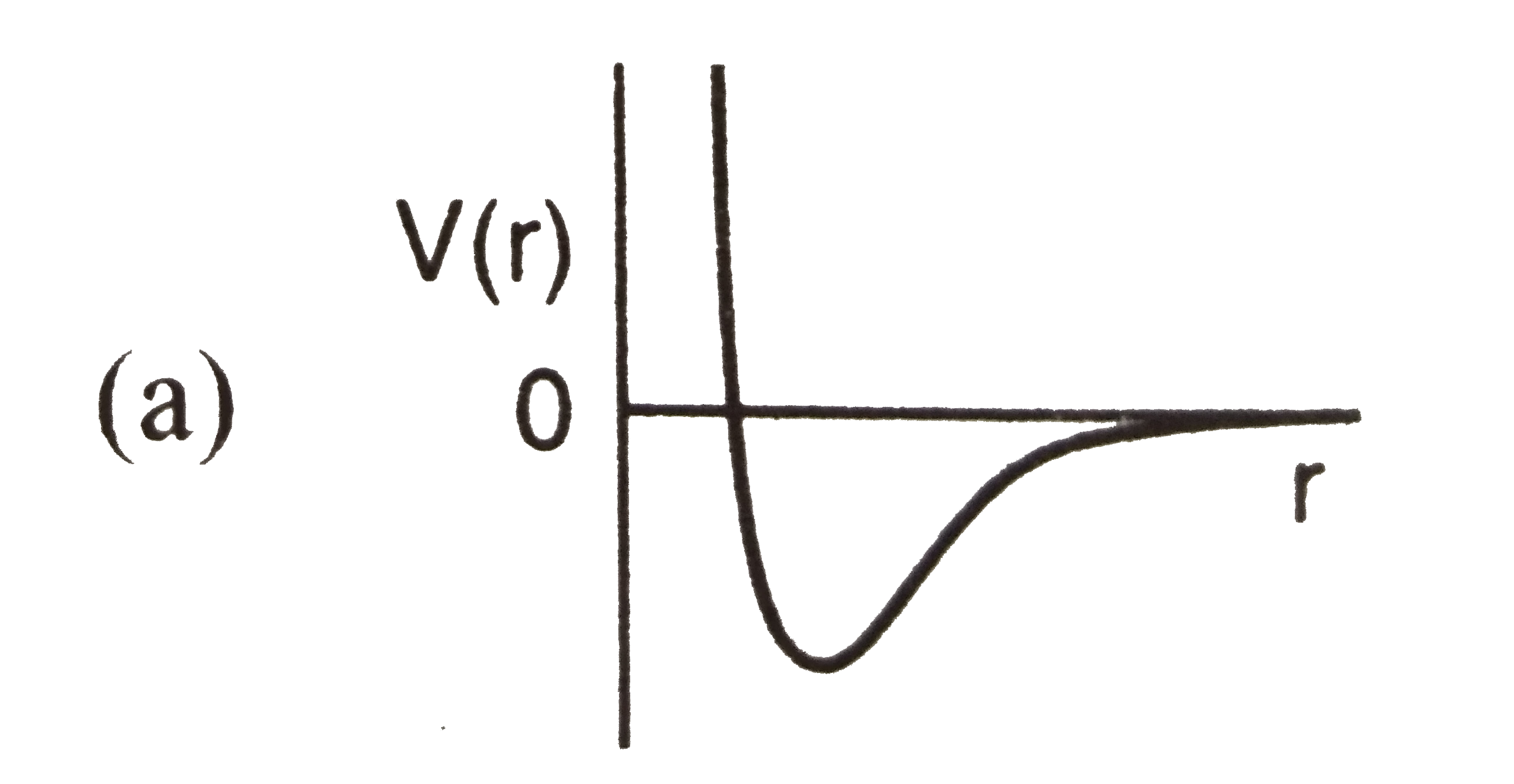

The correct Answer is:C
The given equation is : P(V−b)=RT. On comparing it with van der Waals' equation, i.e., [P+aV2][V−b]=RT, we get :
a=0
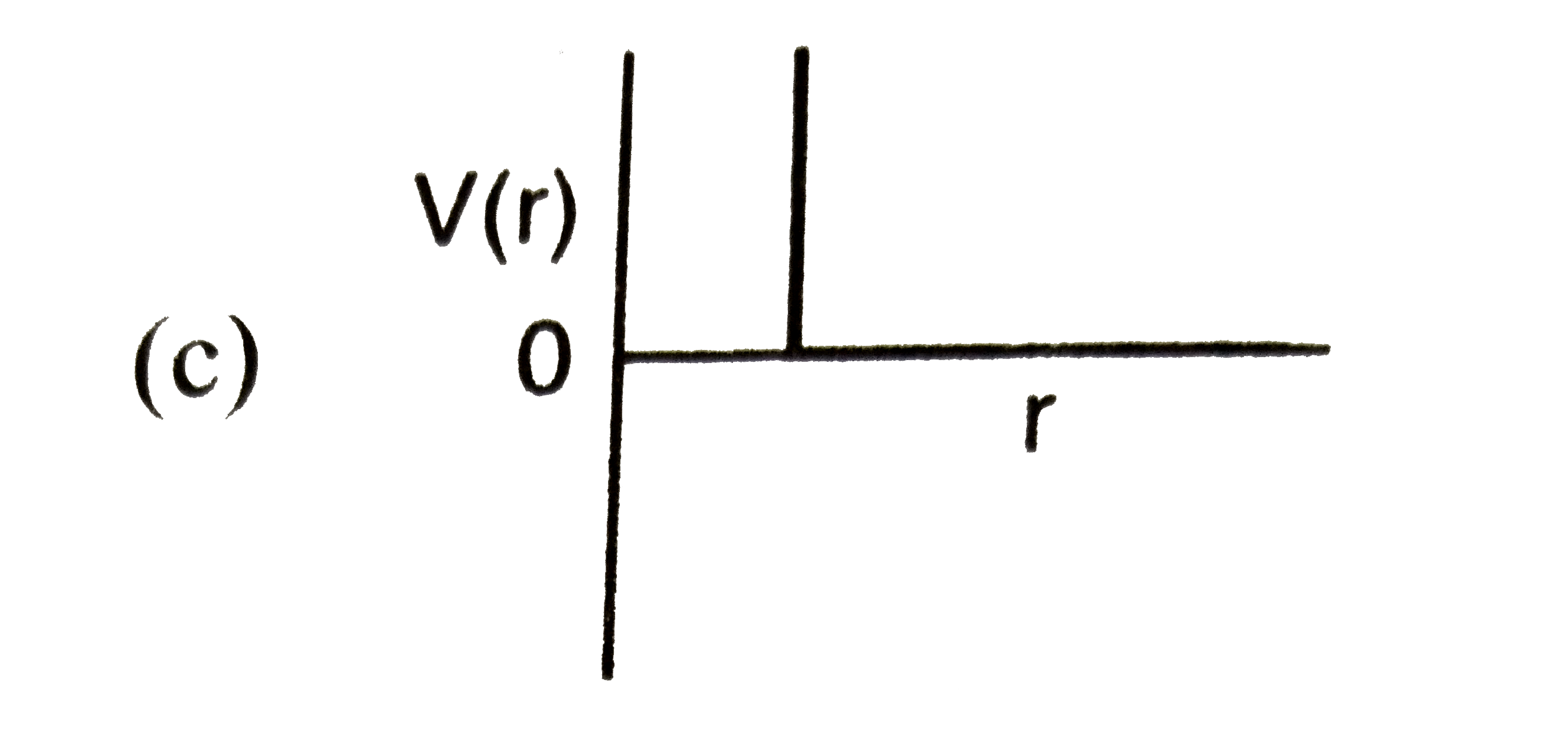
Hence, only repulsive forces are present which are contributive only at very close distance. Thus, potential energy will increases abruptly i.e., graph (c) is correct. Dominance of repulsive forces can be confirmed using compressibility factor.
P(V−b)=RT
PV=Pb+RT
PVRT=PbRT+1
Z=PbRT+T, i.e., Z>1 (Repulsive forces)
Topper's Solved these Questions
- STATES OF MATTER (GASES AND LIQUIDS)BOOK - OP TANDONCHAPTER - STATES OF MATTER (GASES AND LIQUIDS)EXERCISE - Assertion-Reason
10 Videos
- STATES OF MATTER (GASES AND LIQUIDS)BOOK - OP TANDONCHAPTER - STATES OF MATTER (GASES AND LIQUIDS)EXERCISE - Matrix Matching type questions
7 Videos
- STATES OF MATTER (GASES AND LIQUIDS)BOOK - OP TANDONCHAPTER - STATES OF MATTER (GASES AND LIQUIDS)EXERCISE - Set 2
40 Videos
- SOLUTIONS (GENERAL AND COLLIGATIVE PROPERTIES)BOOK - OP TANDONCHAPTER - SOLUTIONS (GENERAL AND COLLIGATIVE PROPERTIES)EXERCISE - Self Assessment
31 Videos
- STATES OF MATTER (SOLID STATE)BOOK - OP TANDONCHAPTER - STATES OF MATTER (SOLID STATE)EXERCISE - SELF ASSESSMENT Section VI
3 Videos
Similar Questions
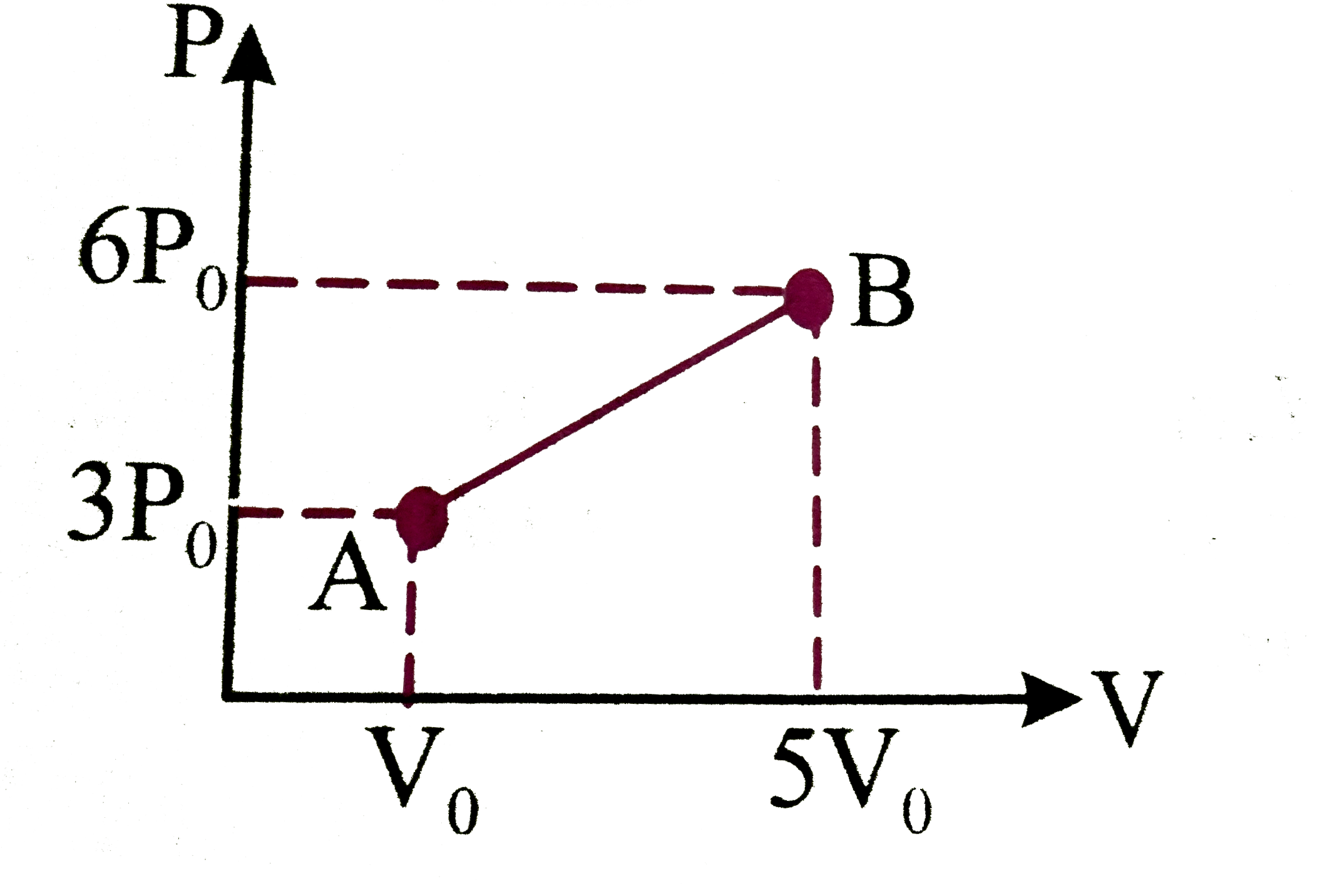
One mole of a monoatomic ideal gas undergoes the process A→B in the given P-V diagram. What is the specific heat for this process?
View SolutionIn a process, temperature and volume of one mole of an ideal monoatomic gas are varied according to the relation VT= K, where K is a constant. In this process the temperataure of the gas is increased by ΔT. The amount of heat absorbed by gas is (R is gas constant).
View Solution
Knowledge Check
One mole of a monoatomic real gas satisfies the equation p(V−b)=RT where b is a constant. The relationship of interatomic potential V(r) and interatomic distance r for the gas is given by
A B
B C
C D
D
One mole of a monoatomic real gas satisfies the equation p(V−b)=RT where b is a constant. The relationship of interatomic potential V(r) and interatomic distance r for gas is given by
A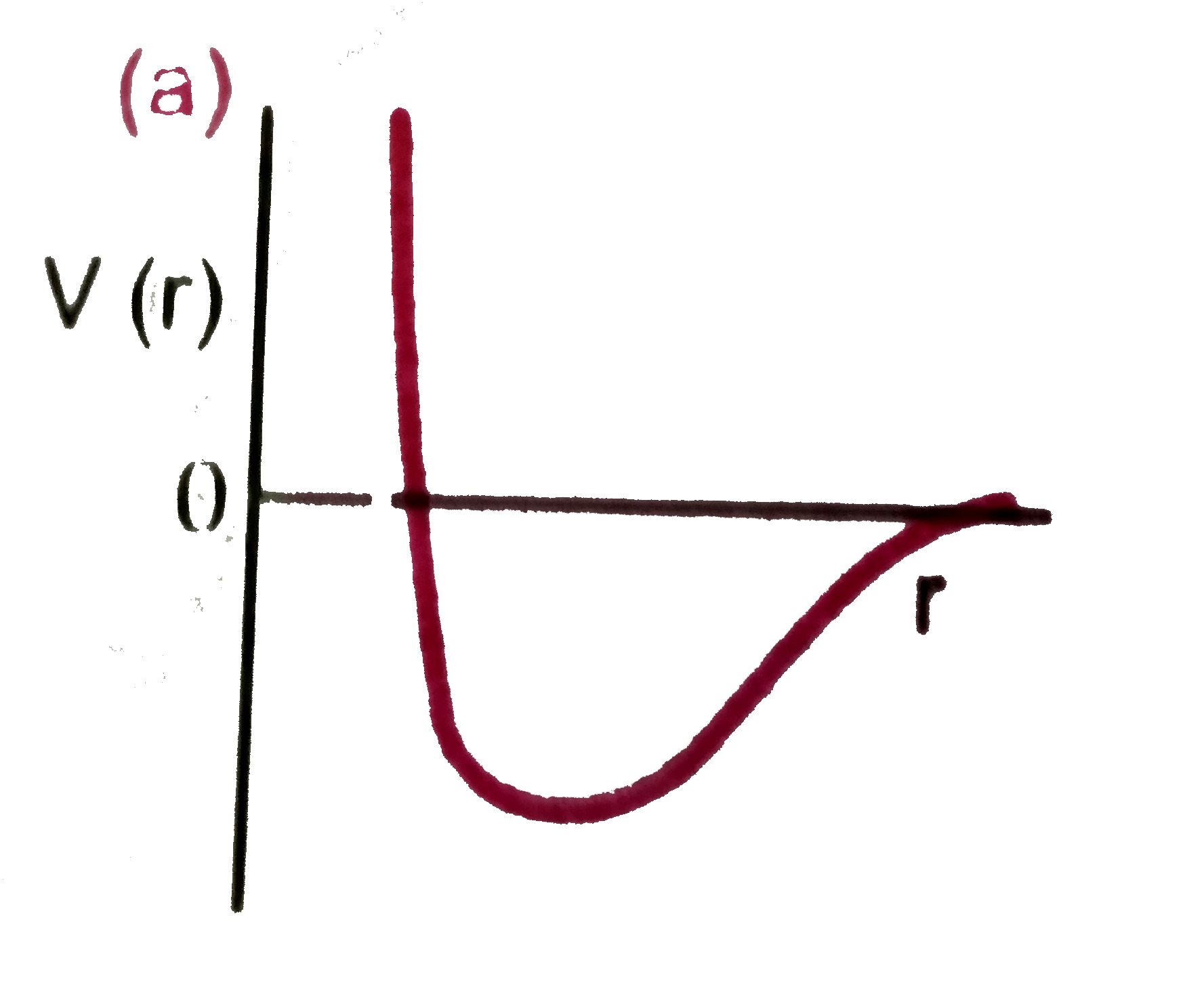 B
B C
C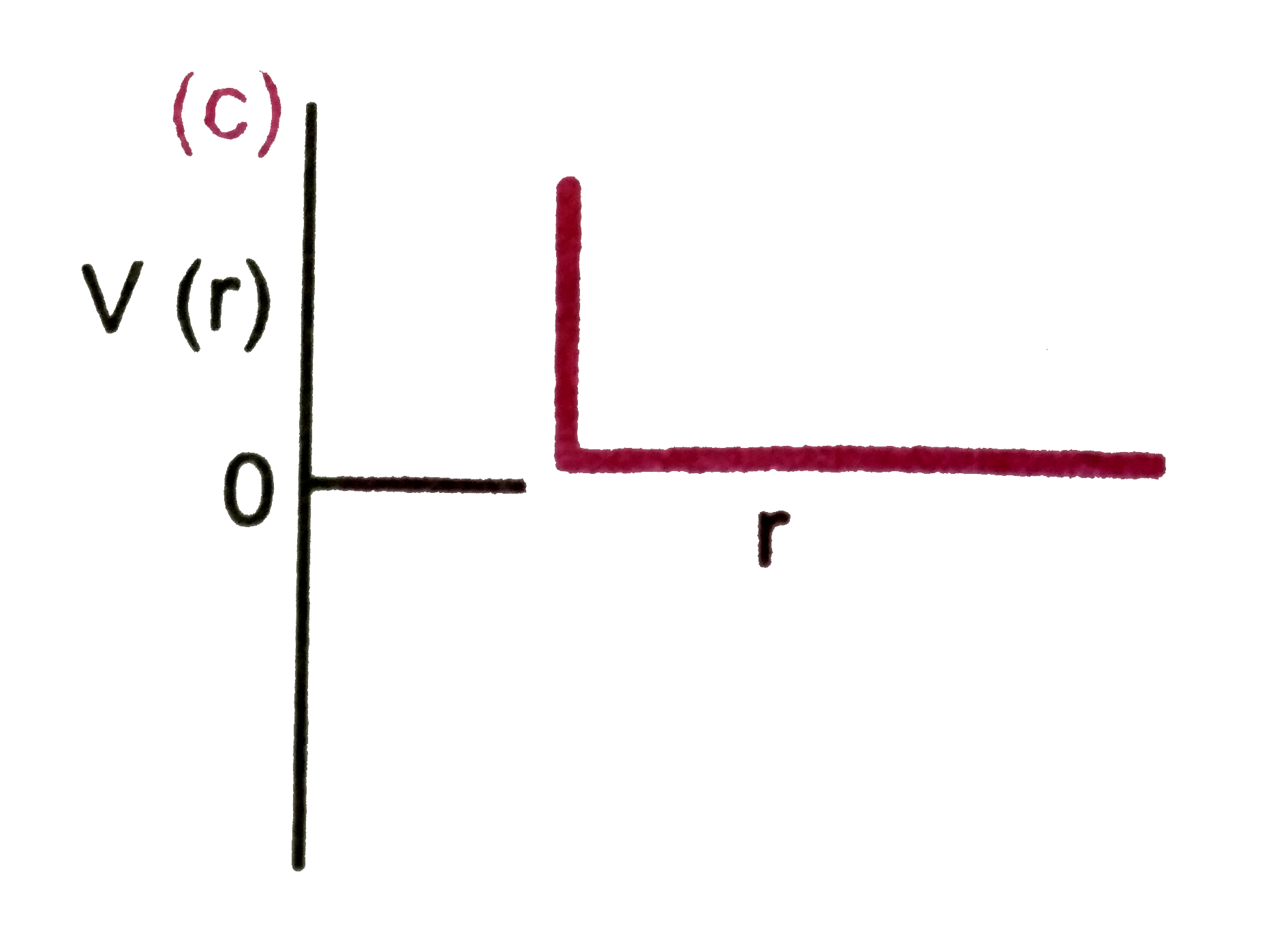 D
D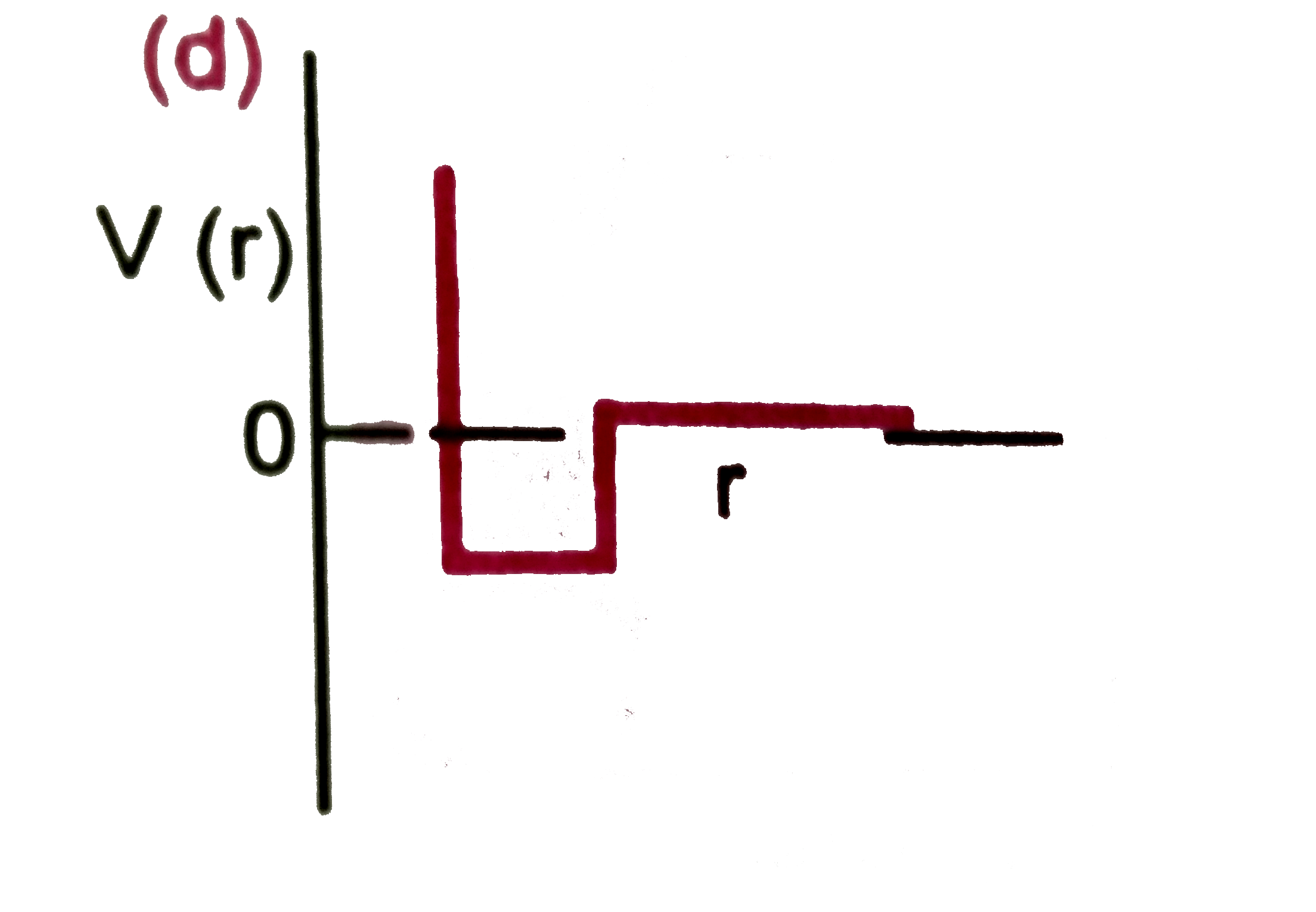
A gas obeys the equation of state P(V−b)=RT (The parameter b is a constnat The slope for an isochore will be .
ANegativeBZeroCR/(V−b)DR/P
One mole of a diatomic gas undergoes 'a process P=P01+(VV0)s, where P0,V0 are constants. The translational kinetic energy of the gas when V=V0 is given by αP0V0β, Find (α+β).
View SolutionOne mole of a monoatomic ideal gas undergoes a thermodynamic process such thatV3T2= constant. Then,
View SolutionIn the gas equation pV=RT, where V refers to the volume of
View SolutionOne mole of a monoatomic ideal gas is expanded by a process described by PV3 = C where C is a constant. The heat capacity of the gas during the process is given by (R is the gas constant)
View SolutionThe equation of state for real gas is given by ((p+aV2(V−b)=RT. The dimension of the constant a is ………………. .
View Solution
