Spin angular momentum of nitrogena to in ground state is:
12h2π
zero
√34(h2π)
√154(h2π)
The correct Answer is:D
N=1s22s22p3
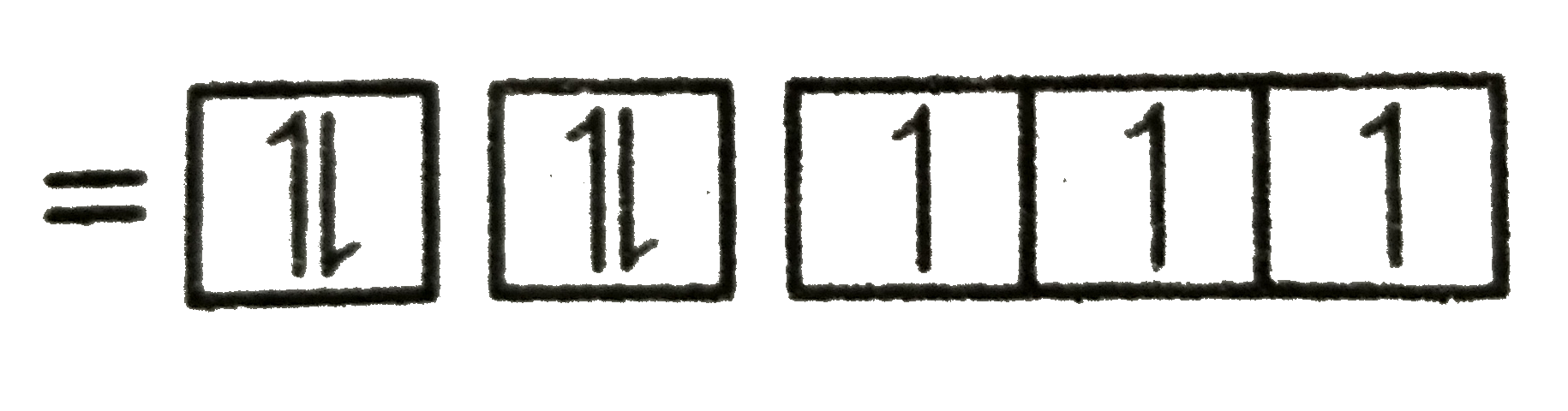
S=∑s=summation of spin quantum number =32
Spin angular momentum =√s(s+1)(h2π)
=√154(h2π)
Topper's Solved these Questions
- ATOMIC STRUCTURE BOOK - OP TANDONCHAPTER - ATOMIC STRUCTURE EXERCISE - Assertion Reason
22 Videos
- ATOMIC STRUCTURE BOOK - OP TANDONCHAPTER - ATOMIC STRUCTURE EXERCISE - Matrix matching Type Question
5 Videos
- ATOMIC STRUCTURE BOOK - OP TANDONCHAPTER - ATOMIC STRUCTURE EXERCISE - Set-2
46 Videos
- AROMATIC HYDROCARBONS (ARENES)BOOK - OP TANDONCHAPTER - AROMATIC HYDROCARBONS (ARENES)EXERCISE - EXAMPLES
24 Videos
- CHARACTERISATION OF ORGANIC COMPOUNDS BOOK - OP TANDONCHAPTER - CHARACTERISATION OF ORGANIC COMPOUNDS EXERCISE - Passage-2
5 Videos
Similar Questions
Knowledge Check
Angular momentum is
Amoment of momentumBproduct of mass and angular velocityCproduct of moment of inertia and velocityDmoment in angular motionAngular momentum is
Amoment of momentumBproduct of mass and angular velocityCproduct of moment of inertia and velocityDmoment in angular motionAngular momentum is
Amoment of momentumBproduct of mass and angular velocityCproduct of moment of inertia and velocityDmoment in angular motion
Spin angular momentum of an electron has no analogue in classical mechanics. Howerver, it turns out that the treatment of spin angular momentum is closely analogous to the treatment of orbital angular momentum
Spin angular momentum =√s(s+1)h
Orbital angular momentum=√l(l+1)h
Total spin of ana tom or ion is a multiple of 12. Spin multiplicity is a factor to confirm the electronic configuration of an atom or ion.
Spin multiplicity =(2∑s+1)
Q. The orbital angular momentum of a 2p-electron is:
View SolutionSpin angular momentum of an electron has no analogue in classical mechanics. Howerver, it turns out that the treatment of spin angular momentum is closely analogous to the treatment of orbital angular momentum
Spin angular momentum =√s(s+1)h
Orbital angular momentum=√l(l+1)h
Total spin of ana tom or ion is a multiple of 12. Spin multiplicity is a factor to confirm the electronic configuration of an atom or ion.
Spin multiplicity =(2∑s+1)
Q. Total spin of Mn2+(Z=25) ion will be:
View SolutionSpin angular momentum of an electron has no analogue in classical mechanics. Howerver, it turns out that the treatment of spin angular momentum is closely analogous to the treatment of orbital angular momentum
Spin angular momentum =√s(s+1)h
Orbital angular momentum=√l(l+1)h
Total spin of ana tom or ion is a multiple of 12. Spin multiplicity is a factor to confirm the electronic configuration of an atom or ion.
Spin multiplicity =(2∑s+1)
Q. Which of the following electronic configurations have four spin multiplicity?
View SolutionSpin angular momentum of an electron has no analogue in classical mechanics. Howerver, it turns out that the treatment of spin angular momentum is closely analogous to the treatment of orbital angular momentum
Spin angular momentum =√s(s+1)h
Orbital angular momentum=√l(l+1)h
Total spin of ana tom or ion is a multiple of 12. Spin multiplicity is a factor to confirm the electronic configuration of an atom or ion.
Spin multiplicity =(2∑s+1)
Q. In any subshell, the maximum number of electrons having same value of spin quantum numbers is:
View SolutionSpin angular momentum of an electron has no analogue in classical mechanics. Howerver, it turns out that the treatment of spin angular momentum is closely analogous to the treatment of orbital angular momentum
Spin angular momentum =√s(s+1)h
Orbital angular momentum=√l(l+1)h
Total spin of ana tom or ion is a multiple of 12. Spin multiplicity is a factor to confirm the electronic configuration of an atom or ion.
Spin multiplicity =(2∑s+1)
Q. Which of the following quantum numbers is not derived from schrodinger wave equations?
View Solution
