The moment of inertia of a body moving with angular velocity ω decreases from l to l3 without any external torque. Calculate the new angular velocity of the body.
l1ω1=l2ω2
ω2=l1ω1l2=lωl3=3ω
Hint : l1ω1=l2ω2
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:AAKASH INSTITUTEChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:Assignment (Section - J) Aakash Challengers Questions
Explore 13 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBook:AAKASH INSTITUTEChapter:SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSExercise:Assignment (Section-D (Assertion and reason))
Explore 5 Videos
- TEST 1Book:AAKASH INSTITUTEChapter:TEST 1Exercise:EXERCISE
Explore 9 Videos
Similar Questions
A flywheel having moment of inertia 20kgm2 rotates about its axis with an angular velocity of 100rads−1. If the moment of inertia of the flywheel is reduced to 10kgm2 without applying external torque, calculate the new angular velocity of the Flywheel.
View SolutionWhat is the torque acting on a body moving with constant angular velocity ?
View Solution
Knowledge Check
If the resultant external torque acting on a body is zero, then angular momentum of the body
AchangesBremains constantCis infinityDzeroTwo points of a rigid body are moving as shown. The angular velocity of the body is :
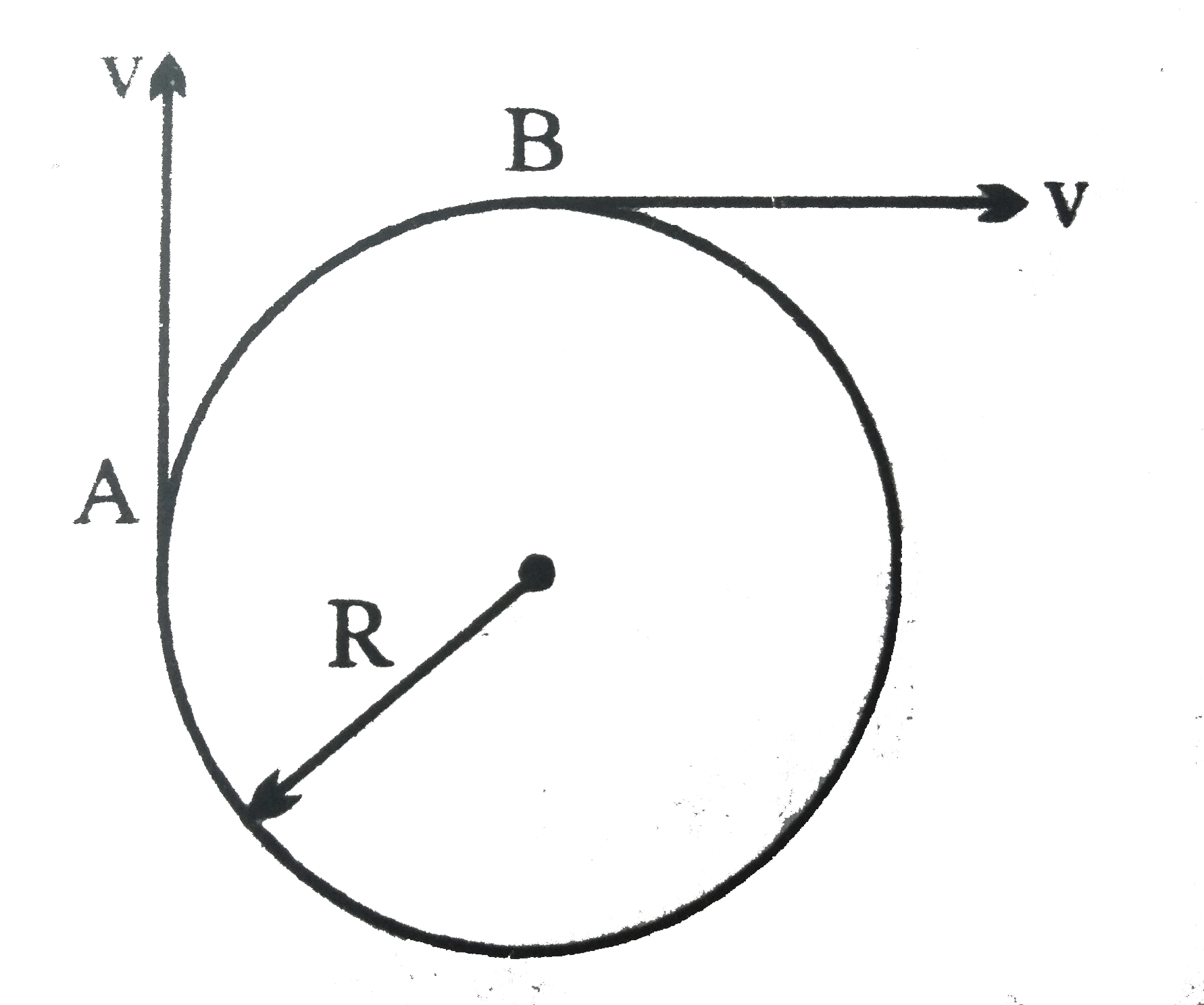 .Av/2RBv/2C2v/RD2v/3R
.Av/2RBv/2C2v/RD2v/3RThe moment of an inertia about an axis of a body which is rotating with angular velocity 1rad s−1 is numerically equal to
Aone - fourth of its rotational kinetic energyBhalf of the rotational kinetic energyCrotational kinetic energyDtwice the rotational kinetic energy
If no external torque acts on a body, will its angular velocity remain conserved ?
View SolutionThe moment of inertia of a rigid body in terms of its angular momentum L and kinetic energy K is
View SolutionIf no external torque acts on a body, will its angular velocity remain conserved ?
View SolutionAn ice skater having moment of inertia l rotating with angular speed ω suddenly opens her arms, which reduces her angular velocity to ω4. Calculate the change in moment of inertia of the dancer.
View SolutionThe moment of inertia (I) and the angular momentum (L) are related by the expression
View Solution