A body of mass 10 kg is kept on a horizontal floor of coefficent of static friction μs=0.5 and coefficient of kinetic friction μk=0.45 as shown in figure.
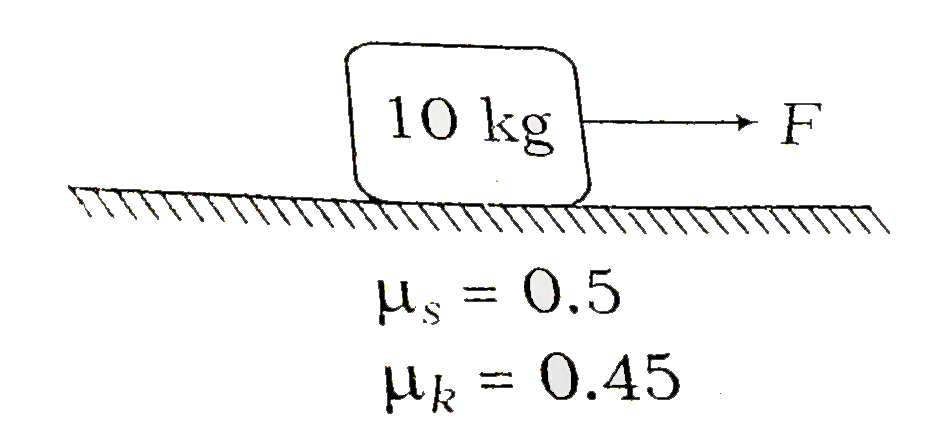
Find the acceleration, force of friction and contact force on the body by the plane when the driving force is (g=10ms−2)
(i) 40 N (ii)60N
FBD of the body:
Normal reaction N=mg=100N
Limiting friction on the body, fL=μsN=0.5×100N=50N
(i) F = 40N is less than the limiting friction so the body is static. So, a = 0.
Force of friction acting on the body is static friction, f = Driving force = 40 N
Contact force is the resultant of force of friction and normal reaction. So,
C=√f2+N2=√(40)2+(100)2=107.7N
(ii) F = 60 N is greater than the limiting friction on the body, so body will start moving. Force of friction acting on the body
=kinetic friction
=μkN=0.45×100N=45N
FBD:

∴ Acceleration of the body is
a=F−fkm=60−4510=1.5m/s2
Contact force, C=√f2+N2=√f2k+N2=√(45)2+(100)2=109.7N
Topper's Solved these Questions
- LAWS OF MOTIONBook:AAKASH INSTITUTEChapter:LAWS OF MOTIONExercise:EXERCISE
Explore 70 Videos
- LAWS OF MOTIONBook:AAKASH INSTITUTEChapter:LAWS OF MOTIONExercise:Assignment (SECTION-A)
Explore 65 Videos
- LAWS OF MOTIONBook:AAKASH INSTITUTEChapter:LAWS OF MOTIONExercise:ASSIGNMENT ( SECTION -J ) Aakash Challengers Questions
Explore 5 Videos
- KINETIC THEORYBook:AAKASH INSTITUTEChapter:KINETIC THEORYExercise:EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
Explore 10 Videos
- MAGNETISM AND MATTER Book:AAKASH INSTITUTEChapter:MAGNETISM AND MATTER Exercise:ASSIGNMENT (SECTION D)
Explore 26 Videos
Similar Questions
A body of mass 10 kg is kept on a horizontal floor of coefficient of static friction μs=0⋅5 and coefficient of kinetic μK=0⋅5 as shown in figure .

Find the acceleration , force of friction and contact force on the body by the plane when the driving force is (g = 10m/s2)
(i) 40 N
(ii) 60 N
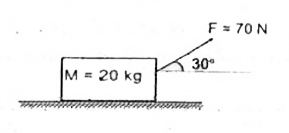
View SolutionA wooden box of mass 20 kg is kept on a rough horizontal surface. The co-efficient of static friction μs=0.41 and co-efficient of kinetic friction μk=0.3 exist between the box and the horizontal surface. A constant force F of 70N is applied to the box at an angle of 30∘ with the horizontal. Find the acceleration of the box on the surface and the frictional force on the box. Take g=10m/s2.
View Solution
Knowledge Check
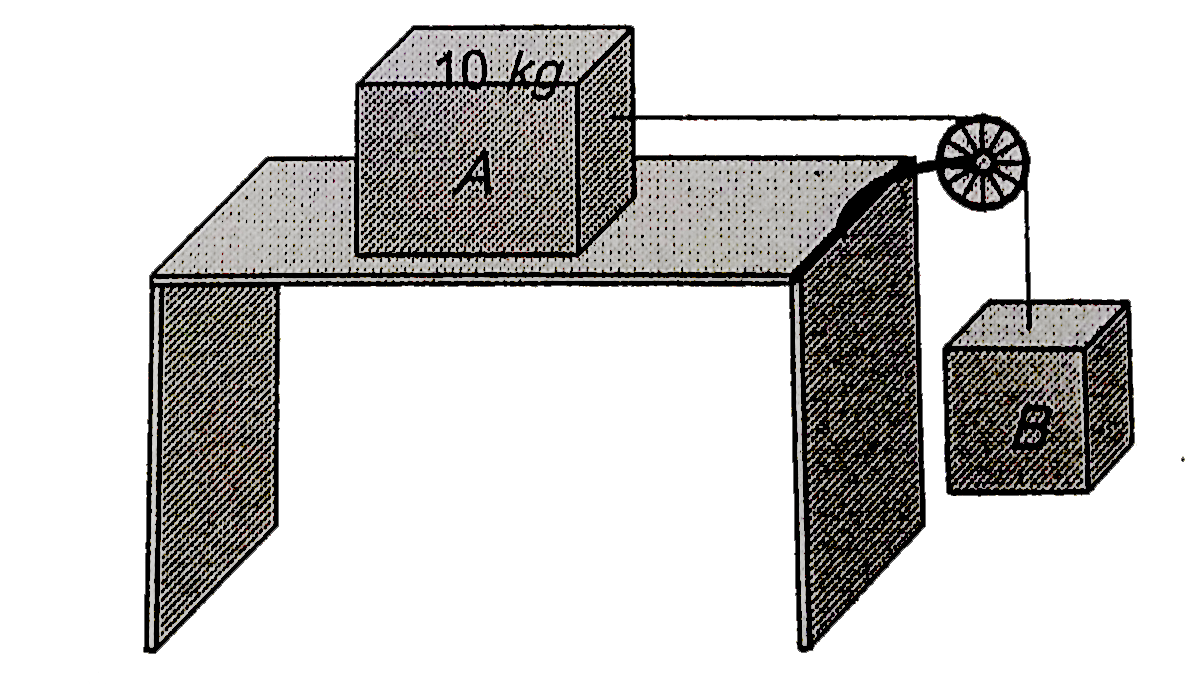
If mass of A=10 kg, coefficent of static friction =0.2 coefficient of kinetic friction =0.2 then mass of B to start motion isA2 kgB2.2 kgC4.8 kgD200 kgA body of mass 2 kg is placed on a horizontal surface having coefficient of kinetic friction 0.4 and limiting coefficient of static friction 0.5. If a horizontal force 2.5 N is applied on the body, the frictional force acting on the body will be (Take, g=10ms2)
A8 NB10 NC20 ND2.5 NA block of mass M is sliding down the plane. Coefficient of static friction is μs and kinetic friction is μk. Then friction force acting on the block is :
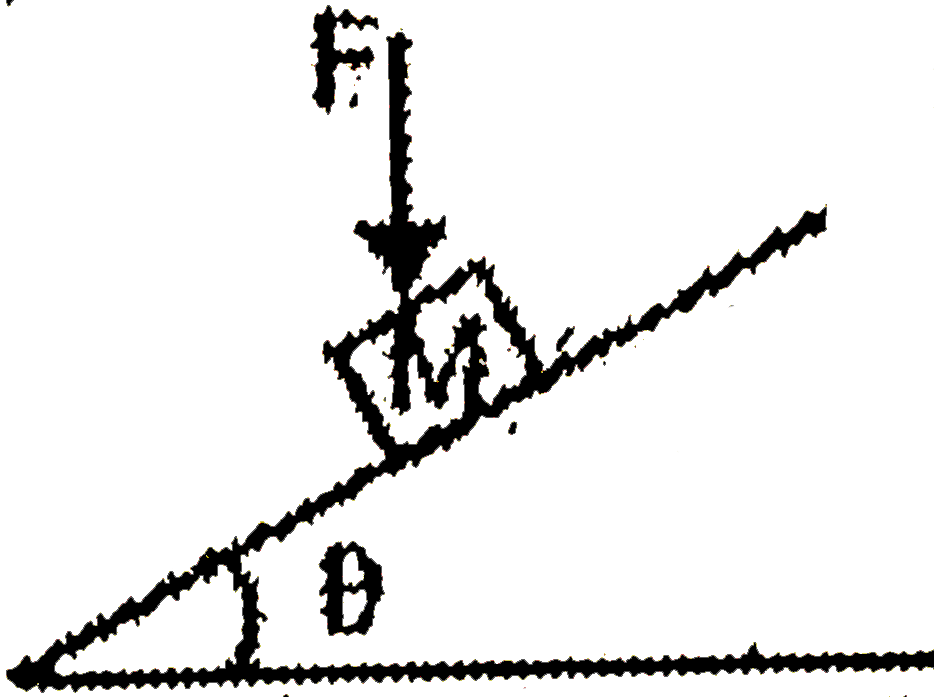 A(F+Mg)sinθBμk(F+Mg)cosθCμsMgcosθD(Mg+F)sinθ
A(F+Mg)sinθBμk(F+Mg)cosθCμsMgcosθD(Mg+F)sinθ
A block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
View SolutionA body of mass 25 kg, is placed on a horizontal surface whose coefficient of friction 0.25. Find the frictional force action on it. Take (g=10ms−2)
View SolutionIn Fig. 6-29, a force →P acts on a block weighing 45 N. The block is initially at rest on a plane inclined at angle θ=15∘ to the horizontal. The positive direction of the r axis is up the plane. Between block and plane, the coefficient of static friction is μs=0.50 and the coefficient of kinetic friction is μk=0.34. In unitvector notation, what is the frictional force on the block from the plane when →P is (a)(−5.0N)ˆi,(b)(−8.0N)ˆi,and(c)(−15N)ˆi?

View SolutionA block of mass 2kg is kept on the floor. The coefficient of static friction is 0.4 . If a force F of 2.5N is applied on the block as shown in the figure, the frictional force between the block and the floor will be.

View SolutionA block of mass 4 kg is kept on a rough horizontal surface. The coefficient of static friction is 0.8. If a force of 19 N is applied on the block parallel to the floor, then the force of friction between the block and floor is
View Solution

