Let P represent radiation pressure, c represent speed of light and l represents radiation energy striking a unit area per second, then will be dimensionless for
x = 0, y = z
x = y = z
x = z = -y
x = y = -z
The correct Answer is:C
To solve the problem, we need to determine the values of x, y, and z such that the expression P(x/y)cz is dimensionless. We will use the dimensional formulas of radiation pressure P, radiation energy per unit area per second I (intensity), and the speed of light c.
1. Identify the Dimensional Formulas:
- The dimensional formula for radiation pressure P is:
(P)=ML−1T−2
- The dimensional formula for intensity I (radiation energy striking a unit area per second) is:
(I)=MT−3
- The dimensional formula for the speed of light c is:
(c)=LT−1
2. Express the Dimensions of the Given Expression:
We need to analyze the expression P(x/y)cz:
P(x/y)=(ML−1T−2)(x/y)=M(x/y)L−(x/y)T−(2x/y)
cz=(LT−1)z=LzT−z
3. Combine the Dimensions:
Now, we combine the dimensions from both parts:
P(x/y)cz=M(x/y)L−(x/y)+zT−(2x/y)−z
4. Set the Exponents to Zero:
For the expression to be dimensionless, all the exponents must equal zero:
- For M:
xy=0(1)
- For L:
−xy+z=0(2)
- For T:
−2xy−z=0(3)
5. Solve the Equations:
From equation (1), we see that x=0.
Substituting x=0 into equations (2) and (3):
- From (2):
z=0
- From (3):
−z=0⇒z=0
Since x=0 and z=0, we can substitute these values into the equations to find y:
- From (1):
0y=0⇒y can be any value.
6. Final Relationships:
We have established that:
x=z=0,y can be any value.
Conclusion:
The expression P(x/y)cz is dimensionless when x=z=0 and y can be any value.
- The dimensional formula for radiation pressure P is:
(P)=ML−1T−2
- The dimensional formula for intensity I (radiation energy striking a unit area per second) is:
(I)=MT−3
- The dimensional formula for the speed of light c is:
(c)=LT−1
We need to analyze the expression P(x/y)cz:
P(x/y)=(ML−1T−2)(x/y)=M(x/y)L−(x/y)T−(2x/y)
cz=(LT−1)z=LzT−z
Now, we combine the dimensions from both parts:
P(x/y)cz=M(x/y)L−(x/y)+zT−(2x/y)−z
For the expression to be dimensionless, all the exponents must equal zero:
- For M:
xy=0(1)
- For L:
−xy+z=0(2)
- For T:
−2xy−z=0(3)
From equation (1), we see that x=0.
- From (2):
z=0
- From (3):
−z=0⇒z=0
- From (1):
0y=0⇒y can be any value.
We have established that:
x=z=0,y can be any value.
The expression P(x/y)cz is dimensionless when x=z=0 and y can be any value.
Topper's Solved these Questions
- UNITS AND MEASUREMENTSBOOK - AAKASH INSTITUTECHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT (SECTION - C)
31 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH INSTITUTECHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH INSTITUTECHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT (SECTION - A)
50 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTECHAPTER - THERMODYNAMICSEXERCISE - ASSIGNMENT (SECTION -D) (Assertion - Reason Type Questions)
10 Videos
- WAVE OPTICSBOOK - AAKASH INSTITUTECHAPTER - WAVE OPTICSEXERCISE - Assignment (Section-J (Aakash Challengers question))
1 Videos
Similar Questions
If P represents radiation pressure , C represents the speed of light , and Q represents radiation energy striking a unit area per second , then non - zero integers x,y,z such that PxQyCz is dimensionless , find the values of x,y,andz.
View SolutionFor a gaseous reaction
aA(g)+bB(g)⇔cC(g)+dD(g)
equilibrium constants Kc,Kp and Kx are represented by the following reation
Kc=[C]c[D]d[A]a[B]b,Kp=Pcc.PdDPaA and Kx=xcC.xdDxaA.xbB
where [A] represents molar concentrationof A,pA represents partial pressure of A and P represents total pressure, xA represents mole fraction of For the following equilibrium relation betwen Kc and Kc (in terms of mole fraction) is
PCl3(g)+Cl2(g)⇔PCl5(g)
View Solution
Knowledge Check
If X represents force, Y represents area and Z represents time. The quantities having same dimensions as coefficient of viscosity in are
AXYZBXZYCYZXDXYZIn the equation of species-area relationship, the letter 'C' and 'Z' represent
AC = Regression coefficient, Z = y-interceptBC = slope of the line, Z = regression coefficientCC = y-intercept, Z = slope of the line (regression coefficient)DBoth B and CWhich of the following graphs correctly represents the relation between In (E) and In (T), where E is the amount of radiation emitted per unit time from a unit area of the body and T is the absolute temperature ?
A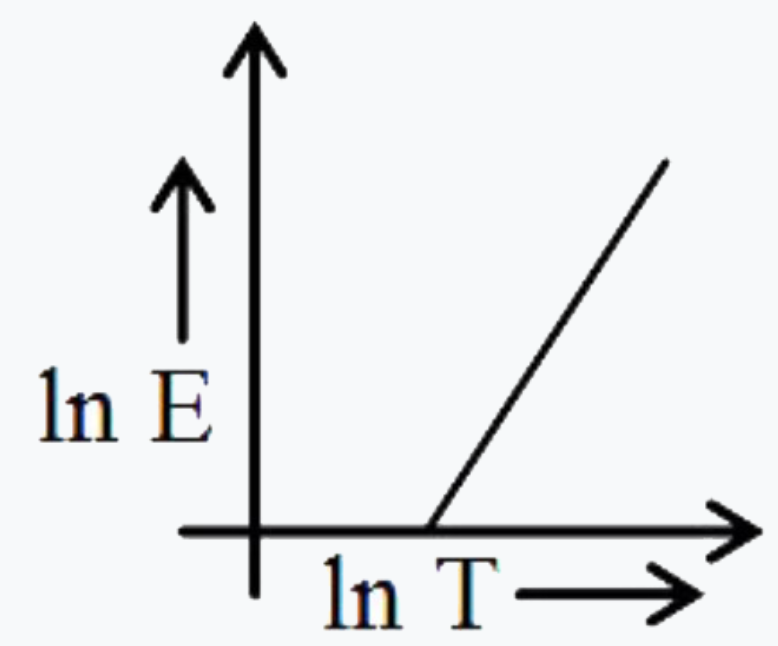 B
B C
C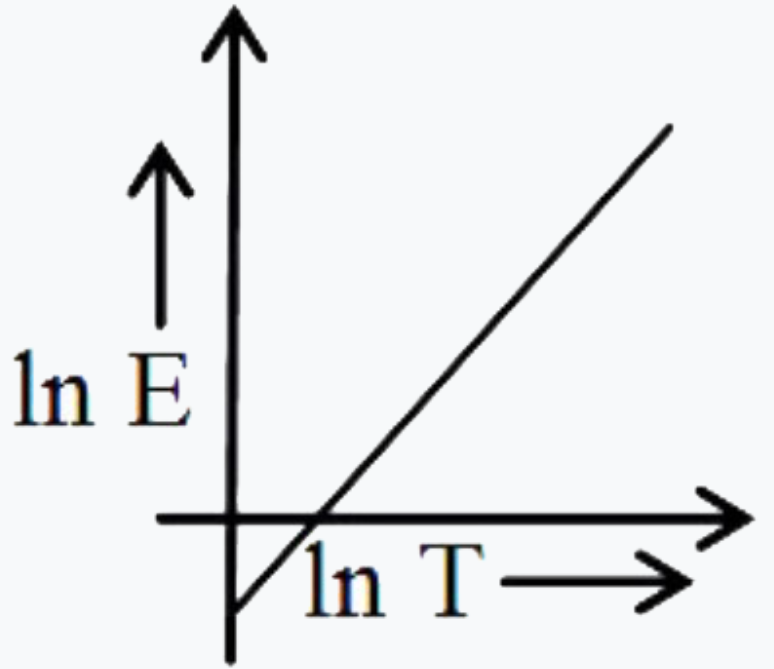 D
D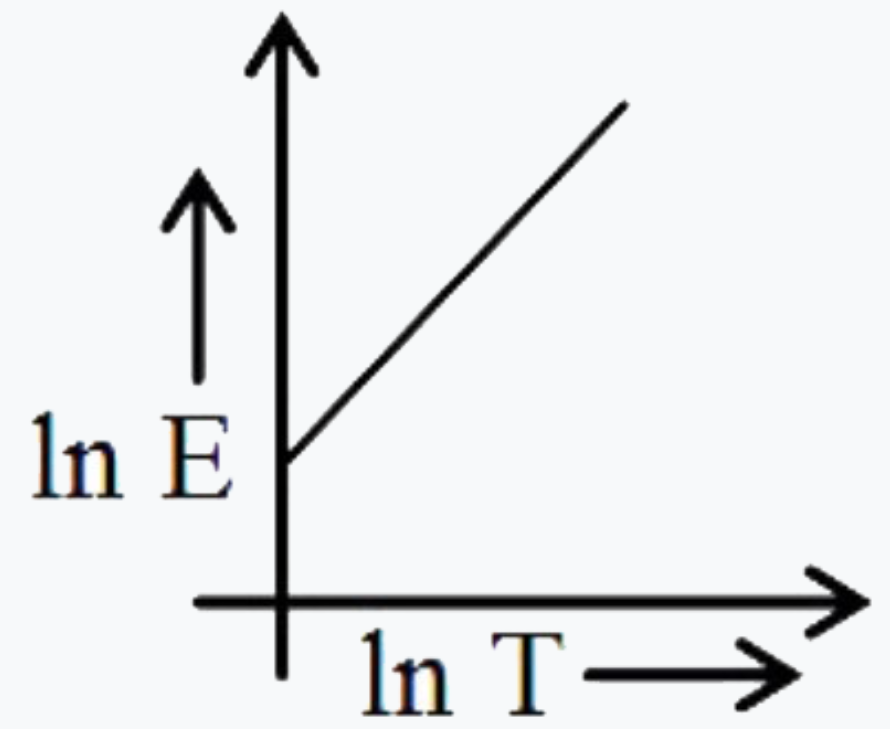
For a gaseous reaction
aA(g)+bB(g)⇔cC(g)+dD(g)
equilibrium constants Kc,Kp and Kx are represented by the following reation
Kc=[C]c[D]d[A]a[B]b,Kp=Pcc.PdDPaA and Kx=xcC.xdDxaA.xbB
where [A] represents molar concentrationof A,pA represents partial pressure of A and P represents total pressure, xA represents mole fraction of A
On the basis of above work-up select the write option
View SolutionThe area of the region represented by |y+x|≤1,|y−x|≤1 and 2x2+2y2≥1 (in square units) is
View Solutionif the equations y=mx+c and xcosα+ysinα=p represent the same straight line then:
View SolutionLet OP.OQ=1 and let O,P and Q be three collinear points. If O and Q represent the complex numbers of origin and z respectively, then P represents
View SolutionIf the energy density and velocity of a wave are u and c respectively then the energy propagating per second per unit area will be -
View Solution
