Find the maximum kinetic enegry of photoelectrons liberated form the surface of lithium by electromagnetic radiation whose electric component varies with time as $E = a (1 + cos ω t) {cos ω}_{0} t$ , where $a$ is a constant, $ω = {6.10}^{14} s^{- 1}$ and $ω_{0} = {360.10}^{15} s^{- 1}$ .(Work function of Lithiuim = 2.39eV)

Video Solution

Text Solution

Verified by Experts

$E = a (1 + cos ω t) {cos ω}_{0} t = a {cos ω}_{0} t + a cos ω t {cos ω}_{0} t$ $\Rightarrow E = a {cos ω}_{0} t + \frac{1}{2} a cos (ω + ω_{0}) t + \frac{1}{2} a cos (ω - ω_{0}) t$ This is a complex vibration consisting of harmonic components of frequencies $ω_{0}, (ω + ω_{0})$ and $(ω - ω_{0})$ .The highest angular frequency is $(ω + ω_{0})$ . now, $h v = ϕ + K_{max}$ so, $K_{max} = \frac{h}{2} π) ((ω + ω_{0}) - ϕ$ = $\frac{6.6 \times 10^{- 34}}{2 π} (6 \times 10^{14} + 3.6 \times 10^{15}) - 2.39 \times 1.6 \times 10^{- 19}$ = $4.41 \times 10^{- 19} - 3.82 \times 10^{- 19}$ = $0.59 \times 10^{- 19}$ J=0.37eV

Updated on:21/07/2023

The maximum kinetic energy of photoelectrons ejected from a metal, when it is irradiated with radiation of frequency $2 \times 10^{14} s^{- 1}$ is $6.63 \times 10^{- 20}$ J. the threshold frequency of the metal is:
A $2 \times 10^{14} s^{- 1}$
B $3 \times 10^{14} s^{- 1}$
C $2 \times 10^{- 14} s^{- 1}$
D $1 \times 10^{14} s^{- 1}$
An electromagnetic radiation whose electric component varies with time as $E = E_{0} (1 + cos ω t) {cos ω}_{0} t (ω = 6 \times 10^{15} rad / s, ω_{0} = 2.8 \times 10^{14} rad / s)$ is incident on a lithium surface (work function =2.39 eV) .
The maximum kinetic energy of a photoelectron liberated from the lithium surface is (h=4.14 xx10^(-15) eV-s)
A2.50eV
B1.90eV
C1.75 eV
D1.50 eV
If the reading of the voltmeters vary with time as: $V_{1} = 20 sin ω t$ and $V_{2} = - 20 cos (ω t + \frac{π}{6})$ then the unknown circuit element $x$ is a:

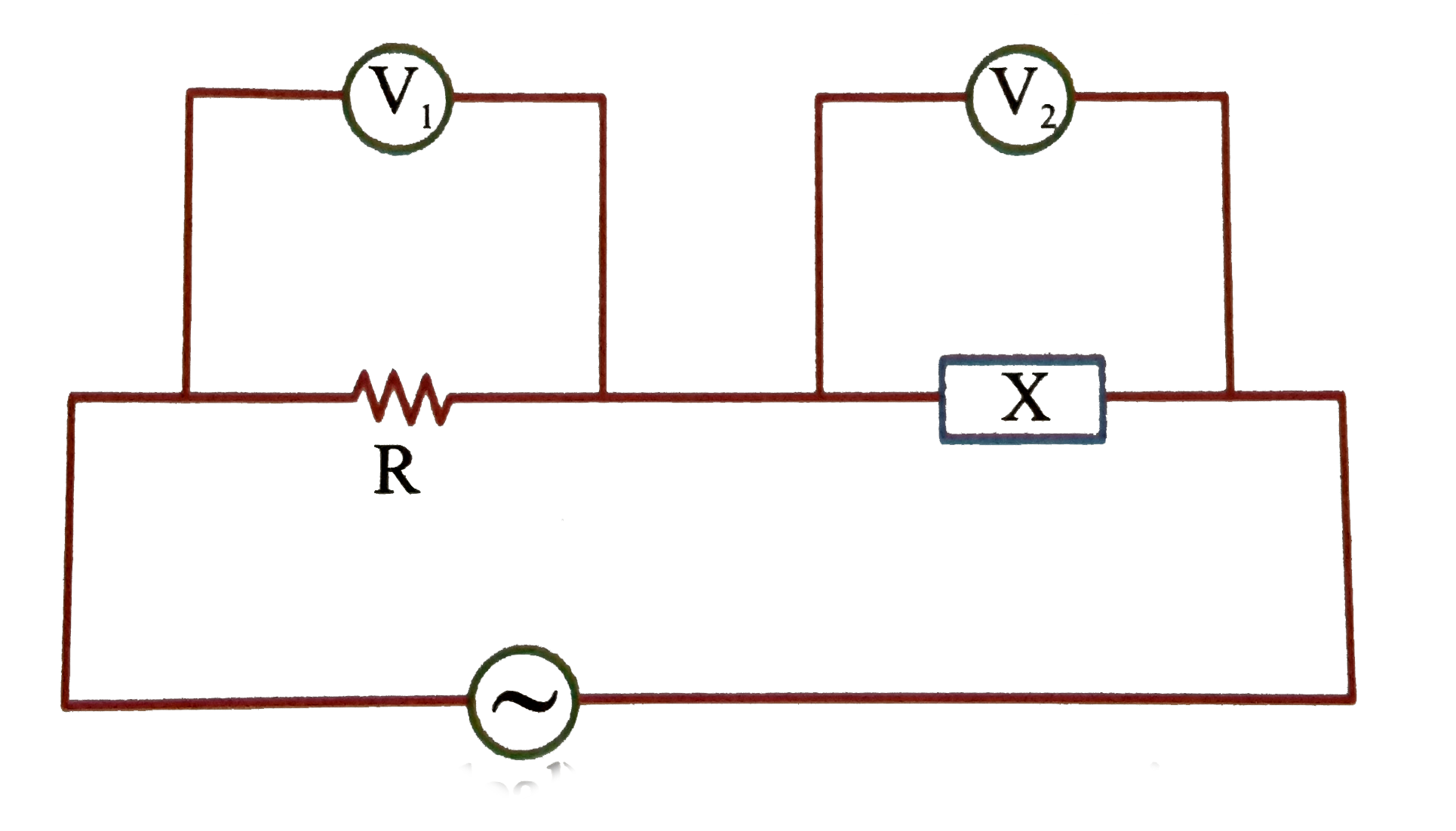Apure (or ideal) inductor
Bpractical inductor
Cpure (or ideal) capacitor
Dpractical capacitor